![]()
Este artículo se centrará en una extensión del modelo original introducido por Estep y. Kritzman (1988), a saber, Time Invariant Portfolio Protection.
El Constant Proportion Portfolio Insurance (CPPI) y la Time-Invariant Portfolio Protection (TIPP) son dos de las estrategias de protección de cartera más conocidas que juegan un papel importante en el ámbito de la gestión de las inversiones y la mitigación de riesgos. Estas estrategias están diseñadas para abordar el desafío fundamental de equilibrar la búsqueda del crecimiento financiero con el imperativo de la protección del capital contra las caídas del mercado. Idealmente, la protección garantizada se logra con la prima más baja posible para los inversores.
EL MODELO
CPPI es un enfoque dinámico que se adapta a las condiciones del mercado ajustando activamente la asignación entre activos de riesgo y sin riesgo, esforzándose por preservar un valor mínimo predefinido al tiempo que permite la participación en los aumentos del mercado. Por el contrario, TIPP emplea una metodología más conservadora, en la que se garantiza un porcentaje fijo del valor de la cartera a lo largo del horizonte de inversión y la exposición de riesgo se ajusta en consecuencia. La principal diferencia es que, mientras que en CPPI el Floor (Se trata de una opción sobre tipos de interés. Una cobertura ante posibles bajadas en el nivel de los tipos de interés) base crece a un ritmo constante, en TIPP es una función del valor de la cartera y, por lo tanto, tiene una naturaleza dependiente de la ruta. Estas dos estrategias ofrecen ventajas e inconvenientes distintos, lo que las convierte en herramientas valiosas para los inversores con diferentes apetitos de riesgo, objetivos de inversión y preferencias para la gestión de la cartera.
Ambas estrategias prescriben una asignación al activo de riesgo que es igual al colchón (diferencia entre V0 y F0) multiplicada por un coeficiente de riesgo-aversión m. Cuanto más alto sea el coeficiente, más agresiva será la estrategia y, a la inversa. La asignación a la libre de riesgo se determina de forma residual.
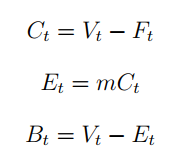
Vamos a mostrar un ejemplo. Si asumimos un capital invertido inicial de 100 $, un Floor inicial de 85 $ y un multiplicador de 4, obtenemos una exposición arriesgada de 60 (4x (100-85)) y una asignación libre de riesgo de 40. Muchos profesionales de las finanzas han introducido nuevas extensiones al modelo vanilla. Por ejemplo, establecer la exposición máxima y mínima evitará, por un lado, la asunción excesiva de riesgos y, por otro, la absorción en un estado de asignación 100% libre de riesgos. En nuestro experimento, forzamos la exposición a estar en el rango del 40 al 120 %.
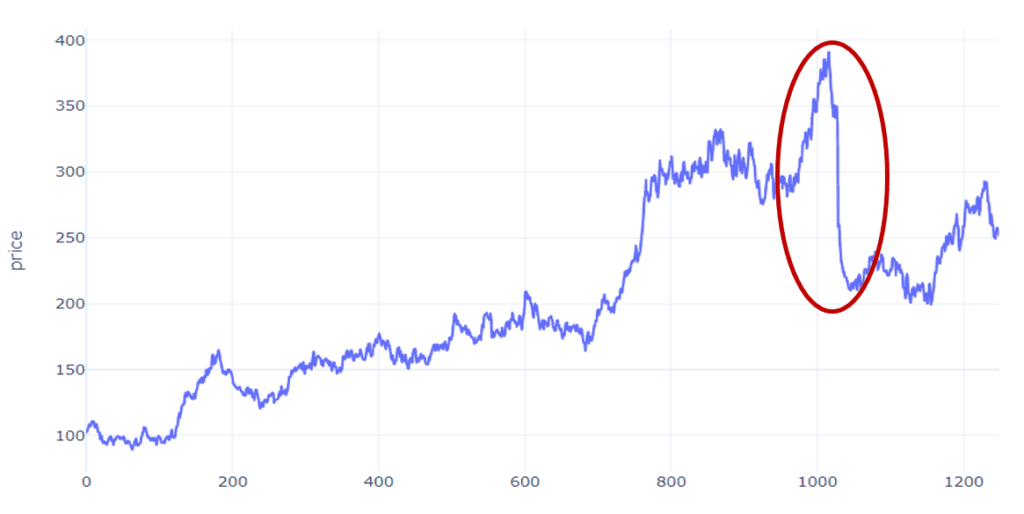
La Figura (a) y la Figura (b) muestran ejemplos de las dos metodologías. En el primer caso, la protección crece con el tiempo a una tasa fija como:
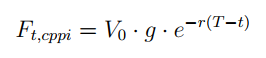
En el segundo caso, el Floor se ajusta hacia arriba para mantener el mismo nivel de protección con respecto al valor de la cartera en cada momento t:
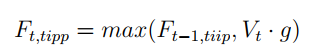
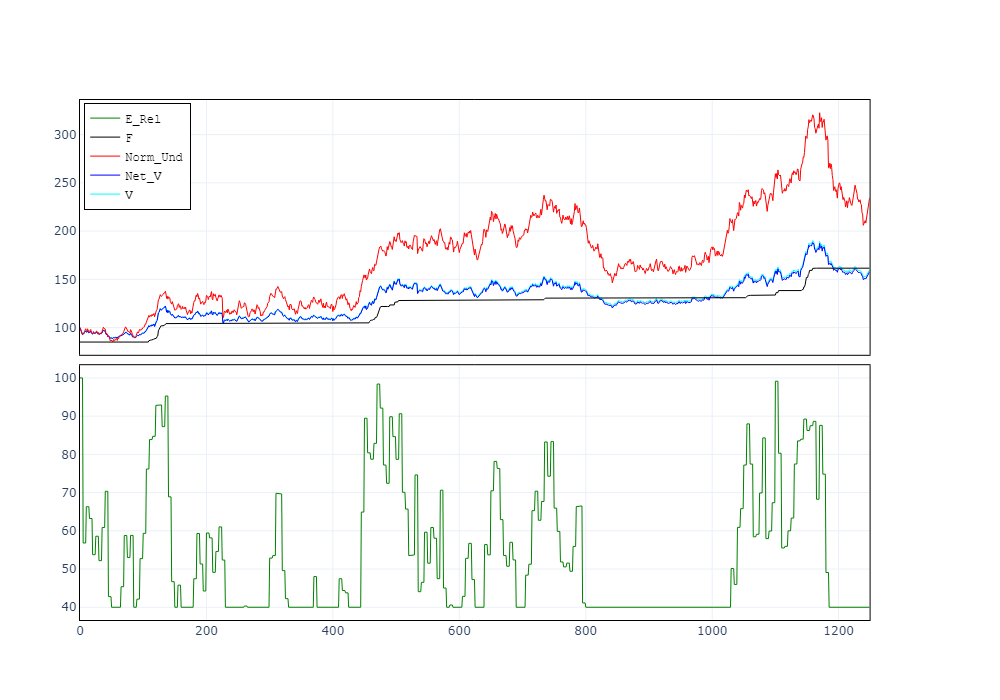
Ahora que hemos explicado la diferencia entre los dos enfoques, nos centramos en las propiedades estadísticas de TIPP. Para hacer eso, seguimos el enfoque metodológico utilizado para CPPI por Khuman et al. (2008) e implementamos el mismo análisis para esta nueva técnica. En particular, investigamos el comportamiento de nuestras métricas de riesgo obtenidas mediante la aplicación de TIPP en dos procesos simulados: el movimiento browniano geométrico (GBM) y el proceso de difusión de salto (JDP). Estos procesos representan un representante de nuestros activos financieros de riesgo. Dado que establecemos un tamaño de salto negativo esperado para reflejar la inclinación negativa de los mercados financieros, permitimos una comparación justa entre los dos procesos mediante la introducción de un compensador positivo al JDP.
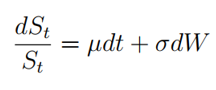
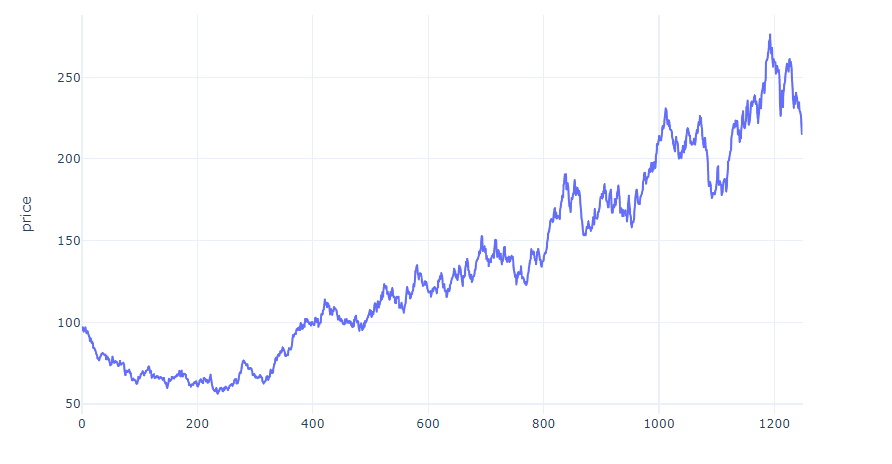
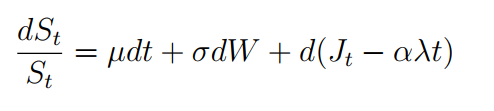
Para validar la eficacia de la estrategia en dos escenarios, consideramos cuatro métricas de riesgo relevantes:
- Pago final promedio
- Probabilidad de brecha, es decir, una brecha en el piso
- Exceso de Sharpe Ratio
- Máximo descuento
Resultados
El primer análisis tiene como objetivo comprender las propiedades de TIPP cuando el multiplicador (m) y la frecuencia de reequilibrio (n) varían. La siguiente tabla muestra la estructura multidimensional de nuestras medidas de interés.
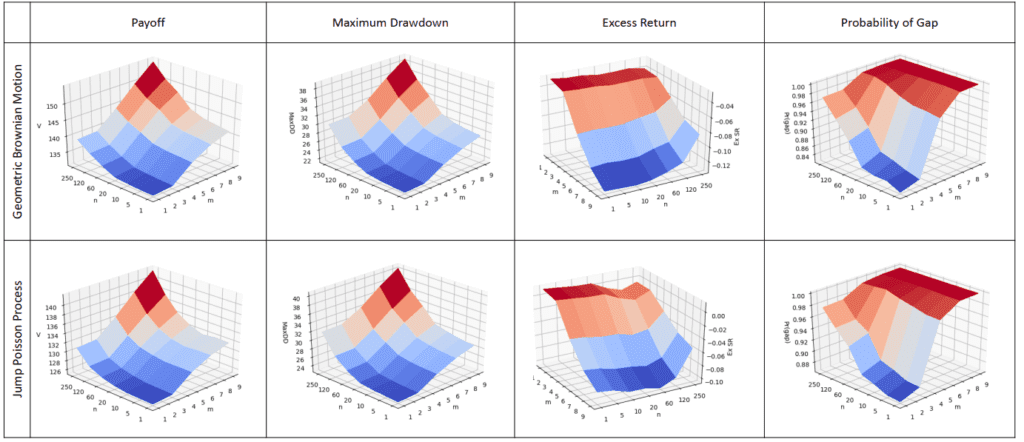
En general, la introducción de saltos negativos en el mercado reduce en un 10% en promedio el pago final y aumenta la probabilidad de una violación del Floor en un 2-4%. Para multiplicadores bajos y reequilibrios frecuentes, el gráfico muestra valores similares de la reducción máxima. En este caso, la presencia de saltos no afecta significativamente a los resultados. Por el contrario, se puede ver un Drawdown un 3% más profundo en la parte superior de la superficie cuando se añade el salto. En términos de Sharpe, la tabla indica una fuerte preferencia por la baja exposición y el reequilibrio diario. De acuerdo con nuestras impresiones iniciales, una m más alta aumenta la volatilidad más de lo que hace en el rendimiento. Teniendo en cuenta la peculiaridad de la protección del capital del TIPP y el impacto de m en la volatilidad y los costos de transacción, creemos que establecer un multiplicador en un rango de 2 a 4 beneficiaría considerablemente la implementación y el seguimiento de dicho enfoque.
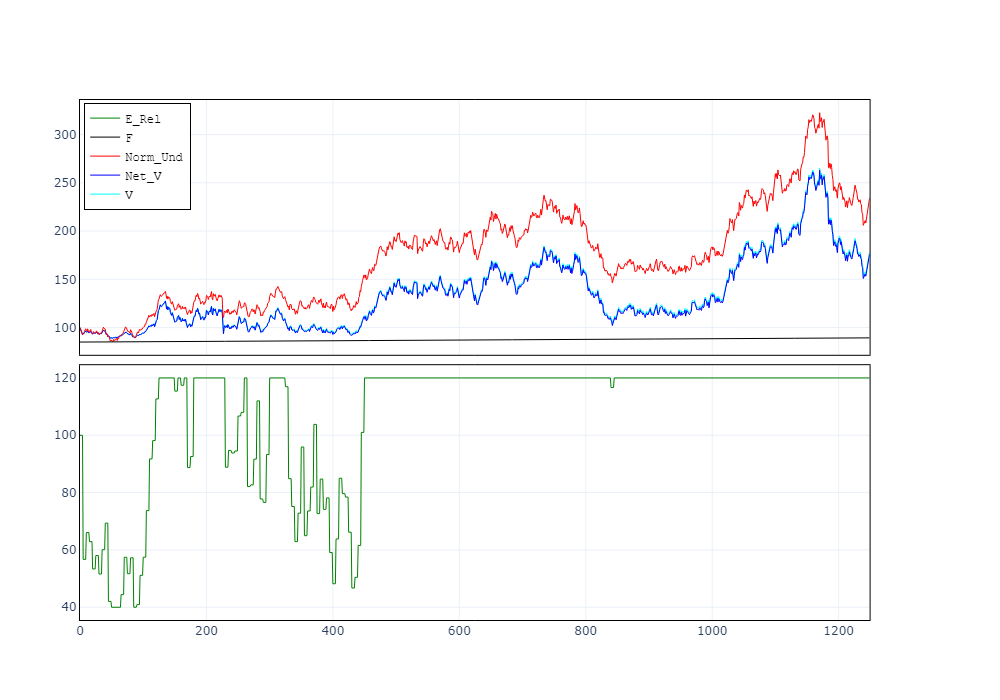
Luego investigamos el impacto de los costos de transacción y el efecto de rotación. Dada la naturaleza más volátil, las tarifas de transacción incurridas en el caso de JDP siempre excederán las pagadas en el escenario de GBM. Por esta razón, llevaremos a cabo nuestro análisis solo para el caso JDP. Los honorarios de gestión no están incluidos en este caso.
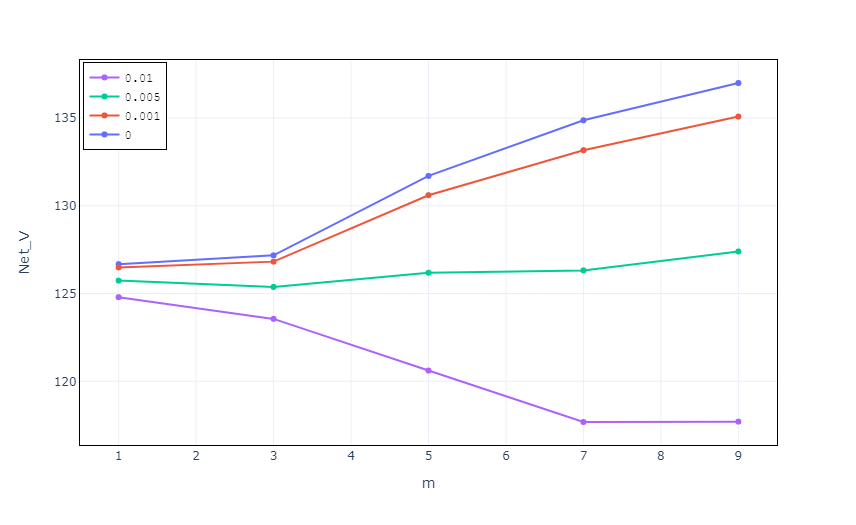
A medida que aumenta la tarifa porcentual, el valor final de la cartera cae exponencialmente. En particular, para el caso de tc = 0,001, el pago neto no se altera significativamente en comparación con el caso de tarifa cero. Por el contrario, vemos un impacto sustancial para los costos de transacción de m ≥ 4 y más altos. Para m = 9, solo un rendimiento semanal del activo de riesgo del -10% daría como resultado un reequilibrio completo de la cartera de la exposición máxima (120) a la mínima (40).
Conclusión
El resultado del estudio revela que la fuerza de TIPP varía significativamente a través de los dos procesos estocásticos. El modelo fue más capaz de mitigar las pérdidas en el GBM en comparación con el caso de JDP, lo que indica una alta sensibilidad a la arriesgada distribución del rendimiento de los activos. Además, vimos que la alta volatilidad y los costos de transacción perjudican el uso de multiplicadores por encima de 5 y que, para aumentar la exposición y evitar el estancamiento, los inversores en TIPP podrían establecer un límite inferior del nivel mínimo de activo de riesgo que se mantendrán en la cartera en su lugar. Por el contrario, el aumento del apalancamiento no tiene resultados positivos en el rendimiento. Por último, destacamos cómo tener una ejecución rentable representa una gran limitación para los gestores de fondos de TIPP, y ese aspecto se vuelve cada vez más importante para los fondos más agresivos.
Autores:
Gianluca Baglini, Baglini Finance
Tony Berrada, Universidad de Ginebra
