
La regresión lineal es una herramienta estadística fundamental en el arsenal de cualquier trader cuantitativo. Aunque el término puede sonar académico, su utilidad práctica en el análisis de mercados es innegable: nos permite identificar relaciones entre variables y detectar ineficiencias explotables en los precios.
En este artículo te mostraré cómo funciona la regresión lineal (simple y múltiple), cómo aplicarla en Python, qué supuestos debes verificar para que los resultados sean fiables, y cómo puedes usarla en estrategias reales de trading como pairs trading, modelos de factores o cobertura dinámica.
¿Qué es la regresión lineal y por qué importa?
La regresión lineal consiste en ajustar una recta que explique cómo una variable (dependiente) se ve influida por una o varias variables independientes. En finanzas, esto suele significar: ¿cómo cambia el precio de un activo cuando cambia el mercado, una materia prima o algún indicador?
En su versión simple (una sola variable explicativa), se expresa como:
Y = β₀ + β₁X + ε
En su versión múltiple (más de una variable explicativa):
Y = β₀ + β₁X₁ + β₂X₂ + ... + βₚXₚ + ε
En ambos casos, β₀ es la constante, β los coeficientes, y ε el error. En trading, esos coeficientes te dicen cuánto se mueve una acción por cada unidad de movimiento del mercado, una materia prima, o cualquier otro factor.
Aplicación práctica 1: Pairs Trading
Pairs Trading busca detectar divergencias temporales entre activos que normalmente se mueven juntos, como dos acciones del mismo sector. Usamos regresión para cuantificar esa relación.
Ejemplo: Regresamos los precios de Shell (RDS.A) contra BP. Si la relación histórica se rompe, operamos esperando reversión: largo en el subvaluado, corto en el sobrevalorado.
Ventaja: Podemos usar el residuo de la regresión (ε) como señal de entrada y el coeficiente β como ratio de cobertura dinámica.
Aplicación práctica 2: Modelos de riesgo y factores
La regresión también permite construir modelos tipo Fama-French, donde explicamos los retornos de un activo en función de factores como:
- Retorno del mercado (Beta)
- Tamaño (SMB)
- Valor (HML)
Ejemplo:
Stock_Return = β₀ + β₁ * Market + β₂ * Size + β₃ * Value + ε
Esto ayuda a entender qué factores están siendo recompensados por el mercado y construir carteras con exposición controlada al riesgo.
Aplicación práctica 3: Cálculo de cobertura (hedge ratio)
Supón que tienes una cartera de acciones tecnológicas y quieres cubrirla con futuros del Nasdaq. Puedes regresar el retorno de tu cartera contra el del futuro para estimar cuántos contratos vender:
Portfolio_Returns = β₀ + β₁ * Nasdaq_Returns + ε
Ese β₁ es el hedge ratio óptimo.
¿Qué necesitas para que funcione bien?
La regresión lineal es poderosa, pero requiere que se cumplan ciertos supuestos clave. Si no se respetan, los resultados pueden ser engañosos:
- Linealidad: la relación entre variables debe ser aproximadamente lineal.
- Independencia de errores: sin autocorrelación, especialmente importante en series temporales.
- Homoscedasticidad: varianza constante de los errores.
- Normalidad de los residuos: importante para construir intervalos de confianza.
- No multicolinealidad: las variables explicativas no deben estar altamente correlacionadas entre sí.
Ignorar estos supuestos lleva a modelos que parecen funcionar… hasta que fallan.
Ejemplo en Python: Regresión simple entre AAPL y SPY
Vamos a ver un ejemplo práctico con Python: ¿cómo se relaciona el retorno diario de Apple (AAPL) con el del S&P 500 (SPY)?
# Importamos librerías
import yfinance as yf
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
# Cargamos datos históricos
data = yf.download(['AAPL', 'SPY'], start='2023-01-01', end='2024-01-01')['Close']
data = data.dropna()
returns = data.pct_change().dropna()
# Definimos variables
Y = returns['AAPL']
X = sm.add_constant(returns['SPY'])
# Ajustamos modelo
model = sm.OLS(Y, X).fit()
print(model.summary())
# Gráfico
plt.scatter(returns['SPY'], returns['AAPL'], alpha=0.5)
plt.plot(returns['SPY'], model.predict(X), color='red')
plt.xlabel('SPY Daily Return')
plt.ylabel('AAPL Daily Return')
plt.title('Regresión lineal: AAPL vs SPY')
plt.grid(True)
plt.show()
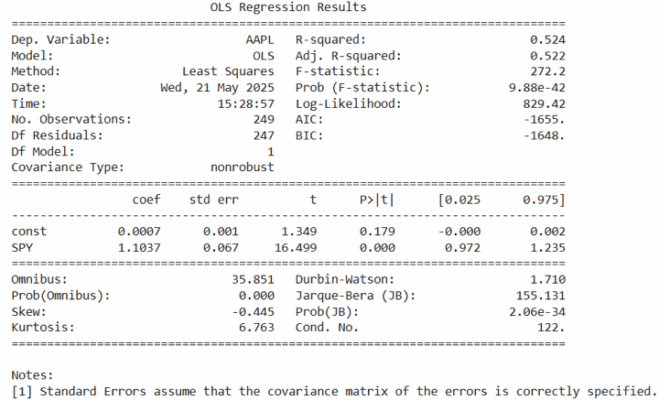
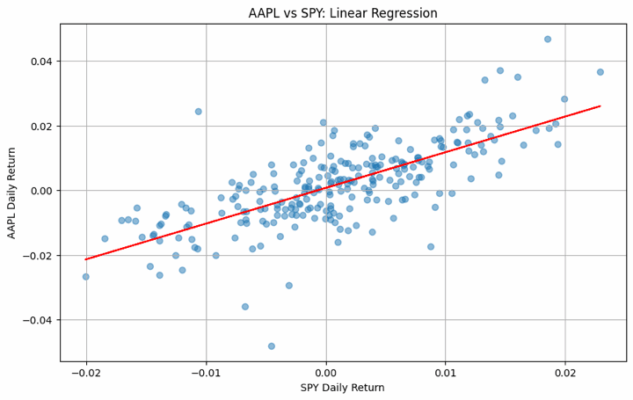
¿Qué te dice esto? El R² te indica cuánta variación de AAPL explica SPY. El coeficiente de SPY te dice la sensibilidad de Apple al mercado (su beta).
¿Cómo evalúas si tu modelo es bueno?
Estas métricas son clave:
- R²: porcentaje de varianza explicada.
- R² ajustado: penaliza modelos con muchas variables que no aportan.
- p-valores: significancia estadística de cada variable.
- RMSE: mide el error promedio de predicción.
- Pruebas out-of-sample: la prueba definitiva: ¿funciona el modelo en datos que no vio durante el entrenamiento?
Limitaciones reales en trading
Como toda herramienta, la regresión lineal tiene límites:
- Solo ve relaciones lineales: muchos patrones de mercado no lo son.
- Sensible a outliers: valores extremos afectan mucho el modelo.
- Confunde correlación con causalidad: que dos activos se muevan juntos no implica que uno cause al otro.
- Regímenes de mercado cambian: lo que funcionó ayer puede dejar de funcionar.
Por eso muchos quants usan ventanas móviles, regularización (Ridge, Lasso) o modelos no lineales como árboles de decisión o redes neuronales.
Conclusión
La regresión lineal es una herramienta simple, potente y muy útil para traders algorítmicos. Sirve para entender relaciones, gestionar riesgo, detectar oportunidades de arbitraje y diseñar estrategias basadas en datos.
Pero su verdadero poder está en usarla bien: respetar sus supuestos, validar fuera de muestra y no confiar ciegamente en el pasado. Dominar lo básico —como esta técnica— te da una base sólida para construir modelos más avanzados y rentables.
En próximos artículos, veremos cómo combinar la regresión con otras técnicas de machine learning para estrategias más robustas y adaptables al mercado real.
