![]()
Recientemente, se han producido avances significativos en las estrategias de trading cuantitativas para la ejecución de los activos en los mercados financieros mediante enfoques de programación dinámica con una velocidad muy alta (en microsegundos). Una de estas técnicas se denomina trading de alta frecuencia (HFT), que ha ganado una atención excesiva por su impacto positivo en la microestructura del mercado. La aparición de HFT ha llevado a la mejora de las numerosas estrategias de trading algorítmico. En consecuencia, hay una creciente demanda de análisis cuantitativo y técnicas de optimización para desarrollar estas estrategias.
Aydoğan et al. (2022) trabajan en la derivación de los precios óptimos para que HFT ejecute las órdenes de compra y venta límite donde los precios medios de los activos en el mercado son generados por un modelo de volatilidad estocástica. Además, añaden componentes de salto en la dinámica de los precios para medir el efecto del número de pedidos de llegada en el precio. Más específicamente, el objetivo es maximizar la riqueza final esperada del inversor al final de la sesión de negociación con inventarios limitados. Los procesos de riqueza e inventario del inversor durante la negociación están cambiando con respecto a las órdenes llegadas y cumplimos. El estudio es la extensión del documento Cartea y Jaimungal (2013), donde estudian el caso de volatilidad constante sin deriva. Aydoğan et al. (2022) consideran la volatilidad estocástica seguida por el modelo de Heston que consiste en saltos en precio o volatilidad y luego generan los precios óptimos de oferta y demanda utilizando la herramienta de control estocástico. Dado que la volatilidad de un activo está fluctuando, la obtención de estrategias óptimas con volatilidad estocástica en la dinámica de precios refleja mejor la realidad en los mercados financieros. Para obtener los precios óptimos, resuelven una ecuación altamente no lineal que se llama ecuación de Hamilton-Jacobi-Bellman (HJB) que propone un enfoque por la condición final. Luego, aplican diferencias finitas y métodos de interpolación/extrapolación. Después de obtener una solución para el problema de control óptimo estocástico, los hallazgos se realizan en datos artificiales de alta frecuencia. Los resultados se pueden aplicar para HFT incluso en un mercado emergente. Los modelos y resultados presentados en este trabajo servirán como modelos extendidos para HFT para una creación óptima de mercado.
- Autores: Burcu Aydoğan, Ömür Uğur y Ümit Aksoy
- Título: Optimal Limit Order Book Trading Strategies with Stochastic Volatility in the Underlying Asset (Estrategias óptimas de trading del libro de órdenes límite con volatilidad estocástica en el activo subyacente)
- Enlace: https://link.springer.com/article/10.1007/s10614-022-10272-4
Resumen:
En las finanzas cuantitativas, ha habido numerosos aspectos y avances relacionados con los problemas de control estocástico y optimización que manejan las variables controladas de la realización del comportamiento de un sistema dinámico para lograr ciertos objetivos. En este documento, abordamos las estrategias de trading óptimas a través de modelos de impacto de precios utilizando el marco de volatilidad estocástica de Heston, incluidos los procesos de salto, ya sea en el precio o en la volatilidad de la dinámica de precios, con el objetivo de maximizar el rendimiento esperado del operador mediante el control de los inventarios. Se consideran dos tipos de funciones de utilidad: cuadrática y exponencial. En ambos casos, los inventarios restantes del creador de mercado se cobran con un costo de liquidación. Con el fin de lograr las cotizaciones óptimas, controlamos el riesgo de inventario y seguimos la influencia de cada parámetro en el modelo a los mejores precios de oferta y demanda. Demos que las métricas de riesgo, incluida la distribución de ganancias y pérdidas (PnL), la desviación estándar y el ratio Sharpe, desempeñan un papel importante para que el operador tome decisiones sobre las estrategias. Aplicamos diferencias finitas e interpolación lineal, así como técnicas de extrapolación para obtener una solución de la ecuación no lineal de Hamilton-Jacobi-Bellman (HJB). Además, consideramos diferentes casos en el modelado para llevar a cabo las simulaciones numéricas.
Ahora, presentamos varias figuras y tablas interesantes:

Citas del documento de investigación académica:
«La figura 2 ilustra los precios óptimos para q=-4, q=0 y q=4, donde cada uno de ellos se obtiene de una simulación y muestra cómo los precios óptimos calculados por las fórmulas de spread cambian según nuestro modelo. Se observa que los diferenciales óptimos tienen diferentes asimetrías para diferentes niveles de los inventarios. Por ejemplo, la estrategia se sigue en el sentido de que el trader compra un activo con un diferencial más bajo y un precio más cercano al precio medio, mientras que vende el activo poniendo un margen de venta más alto y un precio más lejano cuando q = 4. Aquí, S denota el precio medio de la acción que se obtiene mediante el modelo de volatilidad estocástica de Heston, mientras que «oferta y demanda» denota los precios óptimos de oferta y demanda.»
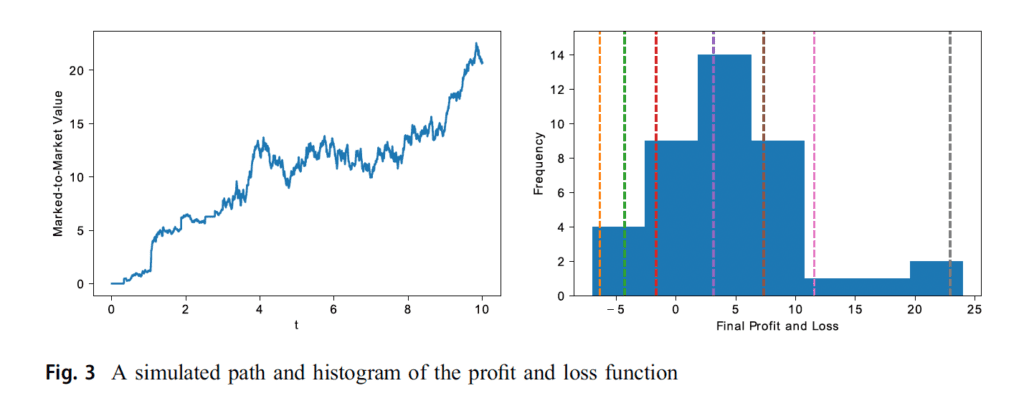
«La figura 3 muestra una simulación de la función de ganancias y pérdidas del creador de mercado en cualquier momento durante la sesión de negociación en el panel izquierdo. El rendimiento de pérdidas y ganancias de la operación se muestra mediante el histograma de nivel de efectivo en el panel izquierdo. Se observa en la Fig. 3 que la estrategia es rentable incluso cuando hay efectos de selección adversos en el modelo debido a las expectativas de los saltos.»
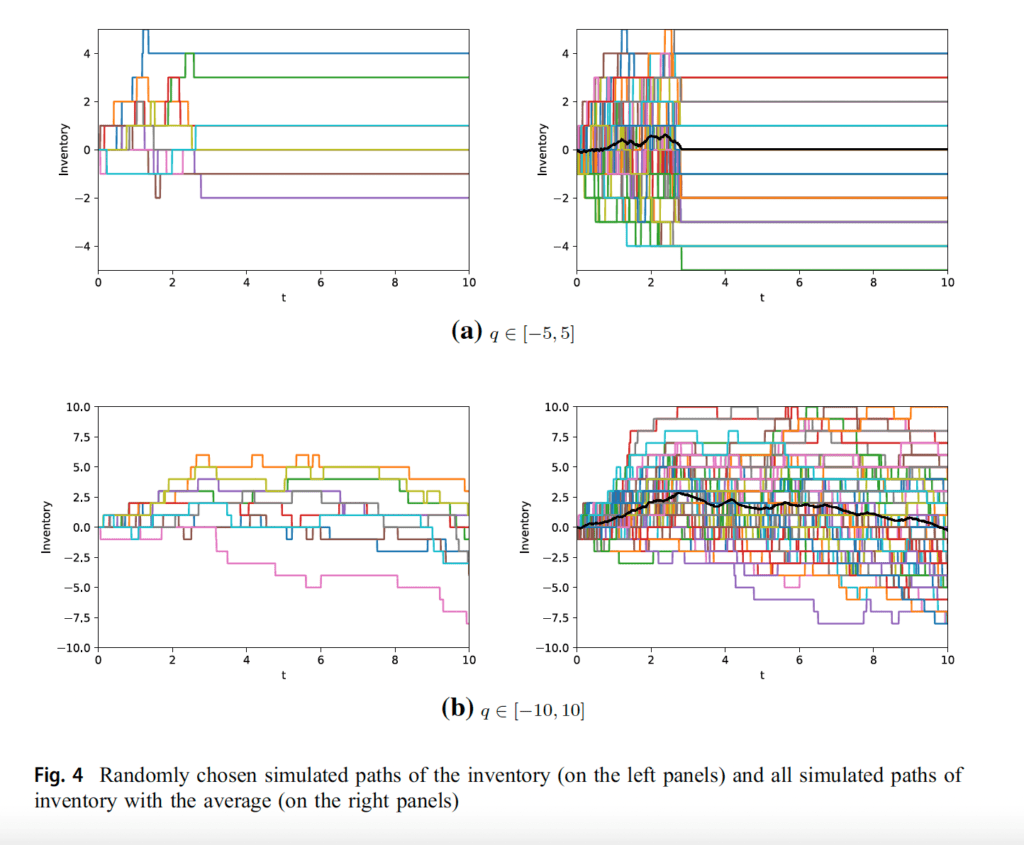
«En la Fig. 4, se pueden ver algunas rutas simuladas del proceso de inventario y el promedio de estas simulaciones para q en [-5, 5] y q en [-10, 10] mientras que los otros parámetros están fijos. En las cifras de la izquierda, se observan 10 rutas seleccionadas al azar del proceso de inventario. Las cifras correctas ilustran todos los caminos simulados con el promedio de estas simulaciones. Se observa que los procesos de inventario cambian para cada operación y el patrón resumido tiende a volver a cero a medida que el tiempo se acerca al final de la operación. La figura muestra claramente que la operación termina en algún momento entre t=2 y t=3 para q en [-5, 5]. Observamos este resultado porque el límite de inventario permitido del comerciante está restringido en un rango pequeño, por lo que los inventarios pueden no volver a cero al final de la operación y es posible que tenga que pagar el costo de liquidación de los inventarios restantes. Por lo tanto, proporcionamos los gráficos para q en [-10, 10] con el fin de ver la evolución temporal del proceso para límites de inventario más grandes.»
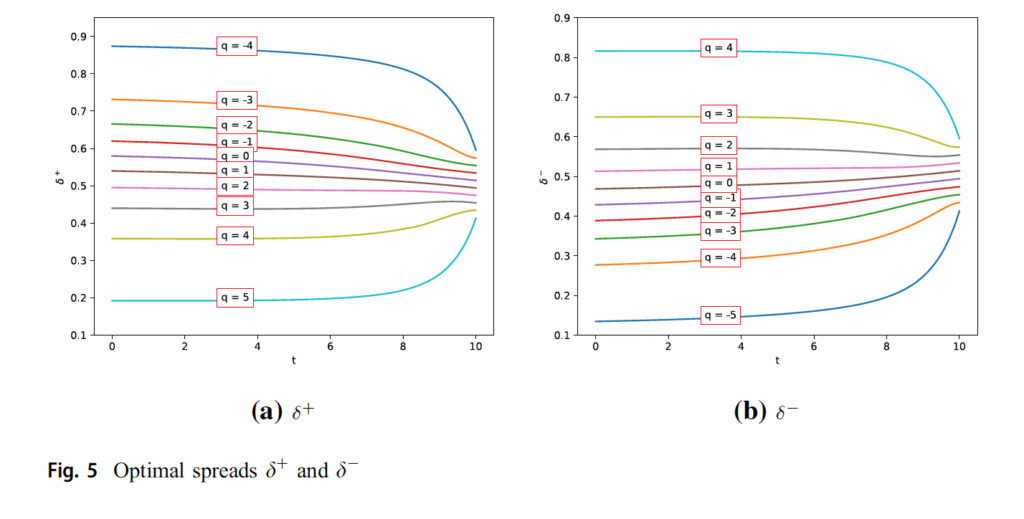
«En la Fig. 5, podemos ver los diferenciales óptimos para el operador dependiendo de los niveles de cada inventario con un parámetro de liquidación dado de 0,01. Este es un pequeño valor de aversión al riesgo de inventario, pero es suficiente para obligar al proceso de inventario a volver a cero al final de la operación.»
«En los niveles de inventario negativos, los valores de los diferenciales de pregunta óptimos son mayores cuando t<T, ya que no puede vender cuando el inventario se acerca al nivel mínimo admitido q, por lo que el comerciante puede querer vender sus activos solo si recibe una gran prima por vender en estos niveles. A medida que se acerca la última vez, se observa que los diferenciales de venta óptimos disminuyen, ya que quiere deshacerse de sus activos en lugar de pagar el costo de liquidación al final de la negociación. En los niveles de inventario positivos, el comportamiento cualitativo del trader es justo lo contrario de la idea de los niveles de inventario negativos. En este caso, el trader quiere reducir el número de acciones en su mano. Porque si todavía tiene los activos cuando se acerca el momento del momento de vencimiento de la operación, entonces tendrá que venderlos a un precio más bajo o pagar el costo de liquidación al final. La probabilidad de vender los activos en el momento del vencimiento es mayor que la del tiempo que está lejos del tiempo terminal. Por lo tanto, el operador aumenta los diferenciales de venta en los niveles de inventario positivos, ya que el tiempo está casi cerca de la hora final. Se puede adaptar una interpretación similar para la propagación de compra óptima (ver Fig. 5b).»
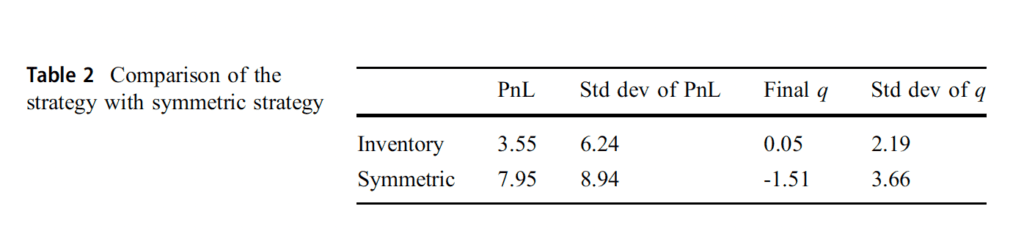
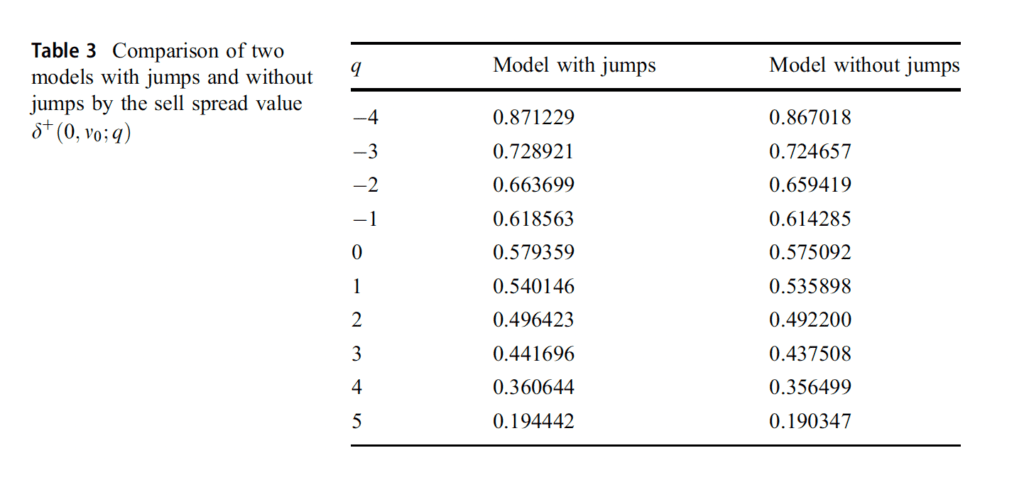
«Para todas las simulaciones, se observa en la Tabla 2 que, cuando comparamos nuestra estrategia con una estrategia de referencia que es simétrica alrededor del precio medio independientemente del inventario, como se hizo en Avellaneda y Stoikov (2008), el beneficio de la estrategia es menor que el de la estrategia simétrica. Por otro lado, los resultados muestran que nuestra estrategia tiene una desviación estándar más baja. También se puede ver que el inventario del operador vuelve a cero más rápidamente que la estrategia simétrica y la desviación estándar del inventario se produce menos en la estrategia. En la Tabla 3, obviamente se ve que el modelo con saltos produce diferenciales de venta más grandes en lugar del modelo sin saltos.»
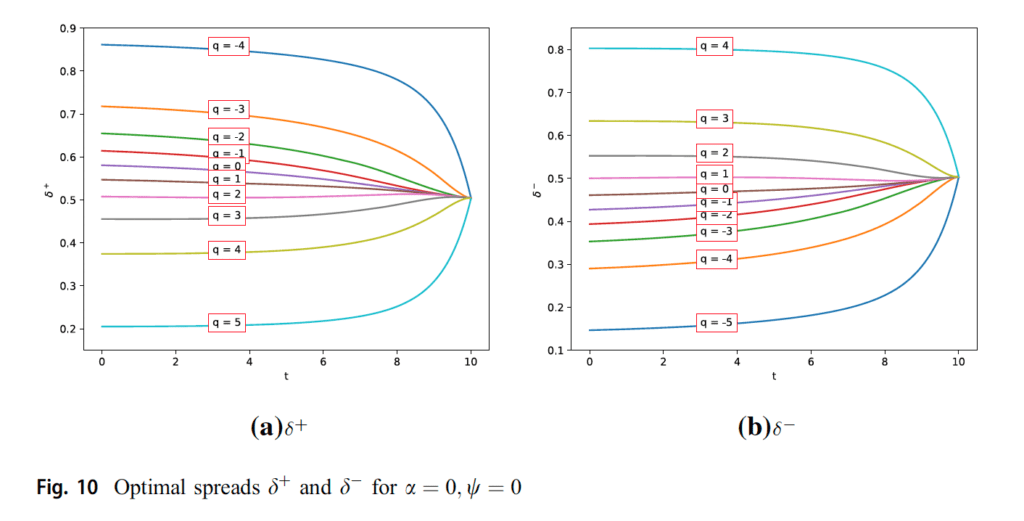
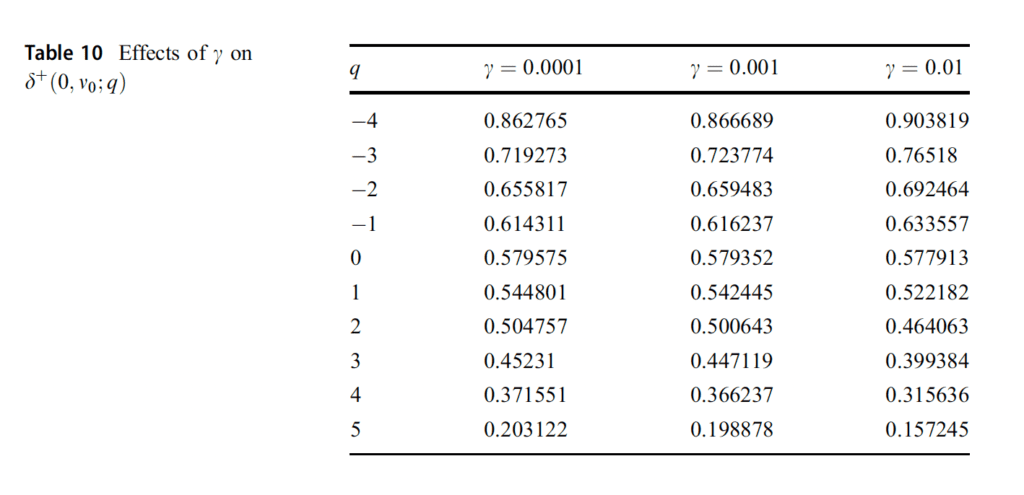
«La figura 10 representa el comportamiento del comerciante por un costo de liquidación cero y una penalización cero de las variaciones en los diferenciales óptimos cuando la estrategia se acerca al tiempo de terminal. En este caso, dado que no hay parámetros de penalización, es fácil entender que los diferenciales convergen a un valor específico cuando t se acerca a la última vez. La tabla 10 muestra los resultados del rendimiento de la estrategia con un parámetro de liquidación 0.01».
