
Bienvenido a esta guía sobre el ratio Sharpe, una métrica financiera desarrollada por el premio Nobel William F. Sharpe en 1966. Esta guía está diseñada para aquellos que buscan comprender cómo se calcula, interpreta y aplica el ratio Sharpe para tomar decisiones de inversión.
En finanzas, lograr altos rendimientos es un objetivo común, pero comprender el riesgo asociado es igualmente importante. El el ratio Sharpe da una medida cuantitativa del rendimiento de una inversión en relación con su riesgo, ofreciendo una herramienta valiosa para comparar y evaluar varias oportunidades de inversión.
A través de esta guía, los lectores cubrirán los conceptos básicos del ratio Sharpe, su fórmula, cálculos prácticos y aplicaciones utilizando ejemplos del mundo real. Exploramos su papel en la comparación de carteras, la evaluación del rendimiento, la gestión de riesgos y la evaluación comparativa, lo que lo convierte en una lectura obligada tanto para los inversores novatos como para los profesionales experimentados.
Ya sea que tenga como objetivo mejorar su estrategia de inversión, profundizar en el trading algorítmico o comprender los fundamentos de los rendimientos ajustados al riesgo, esta guía le da el conocimiento y las habilidades necesarias para navegar por las complejidades de la toma de decisiones financieras. Únase a nosotros para desentrañar las complejidades del ratio Sharpe y dé un paso significativo hacia la optimización de sus inversiones.
Este blog cubre:
- ¿Qué es el ratio Sharpe?
- Fórmula del ratio Sharpe
- ¿Cómo calcular el ratio Sharpe?
- Ejemplo de la relación Sharpe
- Comparación del ratio Sharpe con otras métricas de rendimiento
- ¿Cómo calcular el ratio Sharpe en Excel?
- ¿Cómo calcular el ratio de Sharpe en Python?
- Conceptos erróneos comunes sobre la relación Sharpe
- Limitaciones del ratio Sharpe
- ¿Cómo mejorar el ratio Sharpe?
- Preguntas frecuentes sobre el ratio Sharpe
¿Qué es el ratio Sharpe?
El el ratio Sharpe es una medida utilizada para calcular el rendimiento ajustado al riesgo de una inversión o una estrategia. Desarrollado por William F. Sharpe, un premio Nobel, en 1966, ayuda a los inversores a comprender el retorno de la inversión en comparación con su riesgo.
El ratio Sharpe se utiliza ampliamente en la gestión del riesgo de una cartera para evaluar el rendimiento ajustado al riesgo de las carteras de inversión. Por lo tanto, el ratio de Sharpe juega un papel importante en el análisis de la cartera.
Así es como se aplica:
- Comparación de carteras: Los inversores pueden utilizar el ratio Sharpe para comparar los rendimientos ajustados al riesgo de diferentes carteras. Un ratio Sharpe más alto indica mejores rendimientos ajustados al riesgo, lo que sugiere que la cartera está generando más rendimiento por unidad de riesgo asumido.
- Evaluación del rendimiento: Los gestores de carteras pueden evaluar el rendimiento histórico ajustado al riesgo de sus carteras durante períodos específicos. Al examinar el ratio Sharpe a lo largo del tiempo, los gerentes pueden medir la consistencia y la eficiencia de sus estrategias de inversión.
- Gestión de riesgos: El ratio Sharpe ayuda a comprender la compensación entre el riesgo y el rendimiento. Los gestores de cartera pueden ajustar las asignaciones de cartera para lograr un nivel deseado de rendimiento ajustado al riesgo en función de los conocimientos derivados del ratio Sharpe.
- Evaluación comparativa: El ratio Sharpe se puede utilizar como punto de referencia para evaluar el rendimiento de una cartera frente a un índice de mercado relevante o un grupo de pares. Esta comparación ayuda a identificar si la cartera tiene un rendimiento superior o inferior en relación con su perfil de riesgo.
Fórmula del ratio Sharpe
Matemáticamente, el ratio Sharpe se calcula como:
Aquí hay un desglose de sus componentes:
- Retorno de la cartera o inversión: El rendimiento promedio generado por la inversión durante un período específico.
- Tasa libre de riesgo: El rendimiento de una inversión que se considera que no tiene riesgo, generalmente basado en bonos del gobierno.
- Desviación estándar: una medida estadística de la volatilidad o el riesgo asociado con la inversión, que representa cuánto se desvían los rendimientos del rendimiento promedio.
¿Cómo calcular el ratio Sharpe?
Una vez que vea la fórmula, comprenderá que deducimos la tasa de rendimiento sin riesgo, lo que nos ayuda a averiguar si la estrategia tiene sentido.
Si el Numerador resultara negativo, ¿no sería mejor invertir en un bono del gobierno que le garantice una tasa de rendimiento sin riesgo?
Algunos de ustedes reconocerían esto como el rendimiento ajustado al riesgo.
En el denominador, tenemos la desviación estándar del rendimiento de la inversión. Eso nos ayuda a identificar la volatilidad y el riesgo asociado con la inversión. Por lo tanto, el ratio Sharpe nos ayuda a identificar qué estrategia ofrece mejores rendimientos en comparación con la volatilidad.
Además, un ratio Sharpe más alto indica un mejor rendimiento ajustado al riesgo, lo que sugiere que la inversión o estrategia ha generado más rendimiento por cada unidad de riesgo asumida. Por el contrario, un ratio Sharpe más bajo sugiere que la inversión podría no estar compensando adecuadamente al inversor por el riesgo asumido.
Eso es todo en cuanto al cálculo del ratio Sharpe.
Ejemplo del ratio Sharpe
Tomemos un ejemplo ahora para ver cómo nos ayuda el cálculo del ratio Sharpe.
Has ideado una estrategia y has creado una cartera de diferentes acciones. Después de la prueba, observas que esta cartera, llamémosla Cartera A, dará un rendimiento del 11 %. Sin embargo, le preocupa la volatilidad del 8 %.
Ahora, cambias ciertos parámetros y eliges diferentes instrumentos financieros para crear otra cartera, la Cartera B. Esta cartera da un rendimiento esperado del 8 %, pero la volatilidad ahora cae al 4 %.
Teniendo en cuenta el hecho de que la tasa de rendimiento libre de riesgo es del 3 %, el cálculo de Sharpe Ratio para ambas carteras es el siguiente:
| Cartera A | Cartera B | |
| Tasa de retorno | 11 | 8 |
| Tasa de rentabilidad sin riesgo | 3 | 3 |
| volatilidad | 8 | 4 |
| Ratio Sharpe | (11-3)/8 = 1 | (8-3)/4 = 1,25 |
Por lo tanto, de acuerdo con el cálculo el ratio Sharpe, debemos considerar la cartera B porque, a pesar de que el rendimiento esperado es menor que la cartera B, la volatilidad de la cartera B es menor que la cartera A y, por lo tanto, es menos arriesgada.
Actualmente, la mayoría de los fondos cotizados en bolsa también proporcionan el ratio Sharpe para sus inversiones en sus sitios web.
El ratio Sharpe se puede utilizar en muchos contextos diferentes, como la medición del rendimiento, la gestión de riesgos y para probar la eficiencia del mercado. Cuando se trata de la medición del rendimiento de la estrategia, como estándar de la industria, el ratio Sharpe generalmente se cita como «Sharpe anualizado».
El Sharpe anualizado se calcula en función del período de negociación para el que se miden los rendimientos.
Si hay N períodos de negociación en un año, el Sharpe anualizado se calcula como:
Aquí,
- N: Representa el número de períodos (por lo general, es el número de días o meses de negociación). La raíz cuadrada de N se utiliza para anualizar el ratio. Si está calculando el ratio Sharpe utilizando rendimientos diarios, N sería el número de días de negociación en un año (normalmente 252), y si utiliza rendimientos mensuales, N sería 12.
- E(Rx – Rf): Este es el exceso de rendimiento esperado de la inversión o estrategia, donde Rx es el rendimiento esperado de la inversión, y Rf es la tasa libre de riesgo. El exceso de rendimiento es el rendimiento por encima y más allá de la tasa libre de riesgo, que compensa el riesgo asumido.
- StdDev(x): Esta es la desviación estándar de los rendimientos de la inversión. Mide la volatilidad o el riesgo de la inversión. La desviación estándar indica cuánto se desvían los valores de la media (promedio).
Ratio Sharpe en estrategias intradía
Para una estrategia de negociación intradía, en lugar de usar el cálculo convencional de Sharpe, podemos calcular el nivel de Sharpe para obtener una mejor visión del rendimiento de la estrategia.
En este caso, la tasa libre de riesgo puede considerarse de 0, ya que no hay ningún cargo por intereses. La relación Sharpe se puede calcular siguiendo estos sencillos pasos:
Imagina que tienes una estrategia en la que ejecutas una serie de operaciones, y para cada operación, registras las ganancias y pérdidas (PnL).
He aquí un ejemplo general:
- Operación 1: +0,002 (Beneficio)
- Operación 2: -0,005 (Pérdida)
- Operación 3: +0,003 (Beneficio)
- Operación 4: +0,004 (Beneficio)
- Operación 5: -0,002 (Pérdida)
- Operación 6: +0,001 (Beneficio)
- Operación 7: -0,005 (Pérdida)
- Operación 8: +0,002 (Beneficio)
- Operación 9: -0,004 (Pérdida)
- Operación 10: +0,006 (Beneficio)
Para estas 10 operaciones, puede calcular el ratio Sharpe usando la fórmula:
- Media de PnL: (0,002 – 0,005 + 0,003 + 0,004 – 0,002 + 0,001 – 0,005 + 0,002 – 0,004 + 0,006) / 10
- Desviación estándar de PnL: Calcule la desviación estándar de los valores de PnL.
Digamos que la media es de 0,001 y la desviación estándar es de 0,004. El ratio Sharpe sería entonces:
Ratio de Sharpe = 10 × (0,001/0.004)
Ratio Sharpe ≈ 10 × 0,25
Ratio de Sharpe ≈ 0,25 × 3,162
Ratio de Sharpe ≈ 0,7905
Esto le da una medida de los rendimientos ajustados al riesgo para su estrategia. Cuanto mayor sea el ratio de Sharpe, mejor será el rendimiento ajustado al riesgo de la estrategia.
Aquí hay un ejemplo de código Python simplificado para demostrar el cálculo:
| import numpy as np |
| # Example PnL data for an intraday trading strategy |
| pnl_per_trade = np.array([0.002, –0.005, 0.003, 0.004, –0.002, 0.001, –0.005, 0.002, –0.004, 0.006]) |
| # Number of trades (N) |
| num_trades = len(pnl_per_trade) |
| # Calculate Sharpe Ratio components |
| mean_pnl = np.mean(pnl_per_trade) |
| std_dev_pnl = np.std(pnl_per_trade, ddof=1) |
| # ddof=1 for sample standard deviation |
| # Calculate Sharpe Ratio |
| sharpe_ratio = np.sqrt(num_trades) * (mean_pnl / std_dev_pnl) |
| print(f»Mean of PnL: {mean_pnl}«) |
| print(f»Standard Deviation of PnL: {std_dev_pnl}«) |
| print(f»Sharpe Ratio: {sharpe_ratio}«) |
Salida:
Media de PnL: 0,0002 Desviación estándar de PnL: 0.003938414796731181 Ratio de Sharpe: 0.16058631827165679
Para las estrategias de alta frecuencia, un gran número de pequeñas operaciones exitosas para cantidades específicas suavizan la curva de PnL y la desviación estándar se acerca a cero, lo que aumenta significativamente el ratio de Sharpe, de tal manera que podría oscilar en dos dígitos.
Por sí sola, cualquier estrategia con un «ratio de Sharpe anualizado» de menos de 1 (después de incluir los costos de ejecución) generalmente se ignora. La mayoría de los fondos de cobertura cuantitativos ignoran las estrategias con un ratio Sharpe anualizado de menos de 2.
- Para un trader algorítmico minorista, un ratio Sharpe anualizado superior a 1 es bastante bueno.
- Para el trading de alta frecuencia, como se habló anteriormente, el ratio también puede subir en dos dígitos, especialmente para las estrategias impulsadas por la oportunidad, pero no altamente escalables.
El ratio es utilizado por un individuo cuando está agregando un nuevo instrumento financiero a una cartera existente, y quiere comprobar cómo afecta a la cartera.
Comparación del ratio de Sharpe con otras métricas de rendimiento
Comparemos ahora el ratio de Sharpe con otras métricas de rendimiento a continuación.
| Métrica | Fórmula de cálculo | Se Centra En | Fortalezas | Limitaciones |
| Ratio de Sharpe | (Retorno de la cartera o inversión – Tasa libre de riesgo) / Desviación estándar de la cartera o inversión | Volatilidad tanto hacia arriba como hacia abajo | Medida integral de los rendimientos ajustados por riesgo; adecuado para todas las inversiones | Sensible a valores extremos o fluctuaciones en los rendimientos |
| Ratio de Sortino | (Retorno de la cartera o inversión – Tasa libre de riesgo) / Desviación estándar a la baja | Solo volatilidad a la baja | Se centra en la volatilidad dañina; más adecuado para inversores reacios al riesgo | Ignora la volatilidad al alza. Puede estar sesgado hacia estrategias con más riesgo a la baja |
| Ratio de Treynor | (Devolución de la cartera o inversión – Tasa sin riesgo) / Beta | Riesgo sistemático (relacionado con el mercado) | Evalúa los rendimientos en relación con el riesgo de mercado; Adecuado para carteras diversificadas | Ignora el riesgo no sistemático (específico de la empresa). Supone que la cartera de mercado es eficiente |
| Jensen’s Alpha | Rendimiento de la cartera – (Tasa sin riesgo + (Rendorno del mercado – Tasa sin riesgo)) | Exceso de rendimiento sobre el rendimiento esperado | Mide los rendimientos reales frente a los rendimientos esperados dado el riesgo de la cartera; útil para la gestión activa | Requiere un índice de referencia; ignora otras formas de riesgo |
| Information ratio | (Devolvimiento de la cartera – Retorno de referencia) / Error de seguimiento | Retorno activo en relación con un punto de referencia | Mide la consistencia del rendimiento superior a un punto de referencia | Depende de la precisión de las comparaciones de referencia; la selección de referencia es crucial |
| Ratio calmar | Rendimiento anual compuesto / Reducción máxima | Rendimiento ajustado al riesgo en relación con la reducción | Hace hincapié en el retorno en relación con la pérdida máxima; Adecuado para estrategias de seguimiento de tendencias | Sensible al horizonte temporal; puede que no capture la volatilidad a corto plazo |
| CAPM | Rendimiento esperado = Tasa libre de riesgo + Beta * (Rendimiento del mercado – Tasa libre de riesgo) | Riesgo sistemático (relacionado con el mercado) y rendimiento esperado | Cuantifica la relación entre el rendimiento esperado y el riesgo sistemático | Asume una relación lineal entre el riesgo y el rendimiento; ignora otras fuentes de riesgo |
¿Cómo calcular el ratio de Sharpe en Excel?
Estos son los pasos para calcular la relación Sharpe en Excel utilizando la fórmula:
Asumiendo:
- Rp es el rendimiento promedio de la inversión.
- Rf es la tasa libre de riesgo.
- σ (sigma) es la desviación estándar de los rendimientos de la inversión.
Paso 1: Recopilar datos
En primer lugar, necesitas descargar los datos en línea. Aquí, he tomado los datos de Market Watch para APPLE Inc. (ticker: AAPL). He tomado el precio de cierre diario en este ejemplo.
Puede organizar los datos en la hoja de Excel como se muestra a continuación.
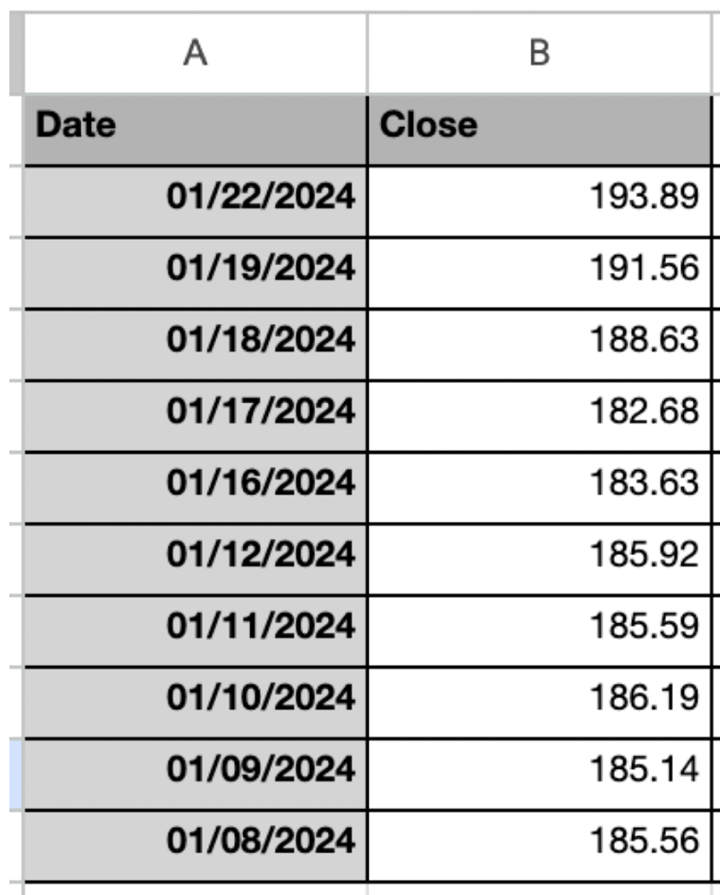
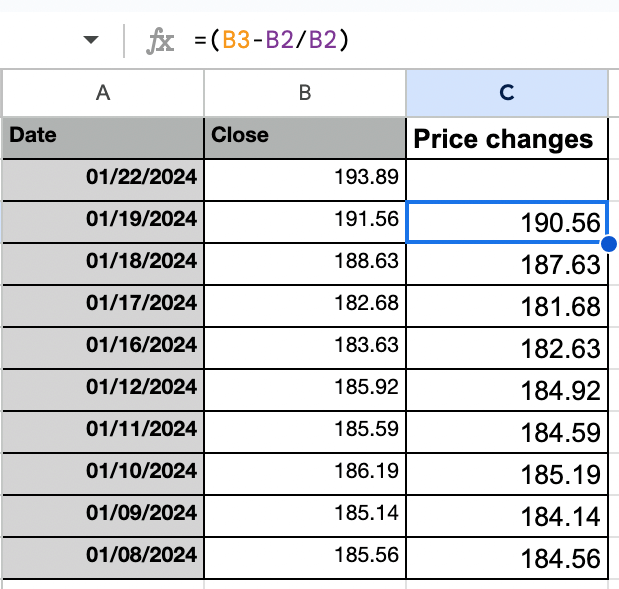
Paso 2: Calcular el cambio de precio para las rentabilidades diarias
Así es como se verá la columna para el cambio diario de precios. Solo tienes que aplicar la fórmula =(B3-B2/B2) y luego arrastrarla hacia abajo a otras celdas de la columna «Cambios de precio».
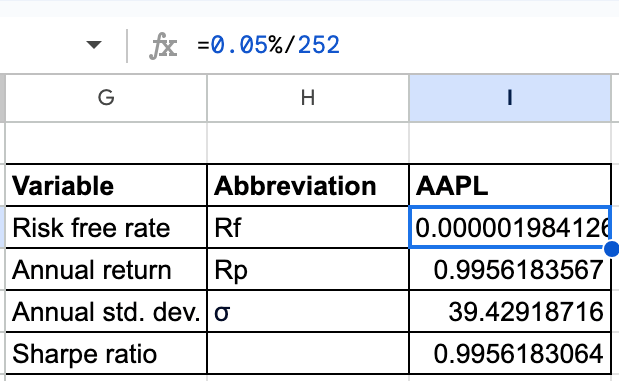
Paso 3: Calcular las variables «tasa libre de riesgo (Rf)», «Rendimiento anual (Rp)», «Desviación estándar anual ()»
Así es como puede organizar la tabla para cada variable necesaria para calcular el ratio Sharpe con la fórmula:
*Ratio Sharpe = Rp – Rf / σ
Así es como calcularás cada variable:
- Tasa libre de riesgo (Rf): Rf se calculará dividiendo el porcentaje de tasa libre de riesgo (0,05 % en este caso) por el número de días de negociación en un año (252 días). Esto dará la tasa diaria libre de riesgo como se muestra a continuación.
2. Rendimiento anual (Rp): El cálculo de Rp requerirá la fórmula que se muestra a continuación.

En esta fórmula,
- B11 es el precio de cierre del último día de negociación.
- B2 es el precio de cierre del primer día de negociación.
- 1/10 significa la constante dividida por el número de operaciones en un día, es decir, 10.
Puedes ver en la imagen de arriba que 0,9956… es el resultado calculado después de aplicar la fórmula.
3. Desviación estándar anual (): Esto se calculará como se muestra a continuación.

En la fórmula,
- C3 es el primer cambio de precio
- C11 es el último cambio de precio
- 252 es el número de días de negociación en un año
- 252^0.5 es la raíz cuadrada de 252
Por lo tanto, al aplicar la fórmula, obtenemos 39,42… como la desviación estándar anual calculada.
Paso 4: Calcular el ratio de Sharpe
Ahora, calcularemos el ratio Sharpe como se muestra a continuación.
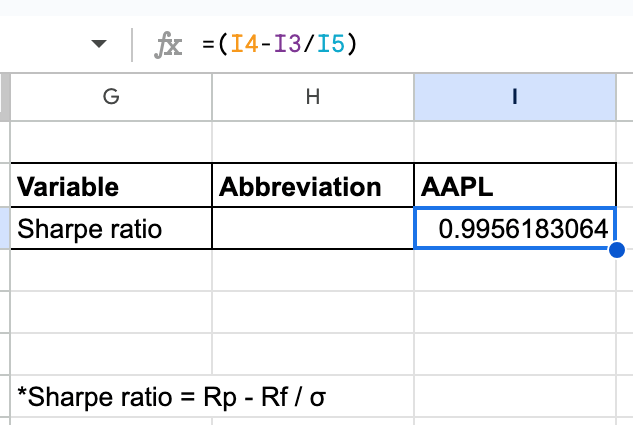
En la fórmula,
- I4 es la rentabilidad anual (Rp)
- I3 es la tasa libre de riesgo (Rf)
- I5 es la desviación estándar anual ()
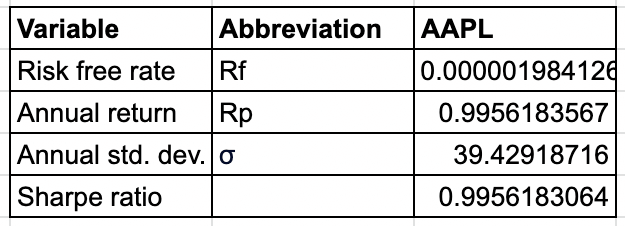
En la imagen, (tomada de la hoja de Excel) podemos ver que el ratio Sharpe calculado es de 0,9956.
Arriba puedes ver cómo se ve toda la tabla con todos los cálculos.
¿Cómo calcular el ratio Sharpe en Python?
Yendo más allá, si desea encontrar el ratio Sharpe por su cuenta con el código Python, a continuación se muestra cómo podemos hacerlo.
Veamos el proceso paso a paso de lo mismo.
Paso 1: Importar las bibliotecas necesarias
| import numpy as np |
| import pandas as pd |
| import yfinance as yf |
| import matplotlib.pyplot as plt |
Paso 2: Obtenga los datos de acciones de AAPL de Yahoo Finance para el período 2022-2024
| # Fetch AAPL stock data from Yahoo Finance |
| aapl_data = yf.download(‘AAPL’, ‘2022-01-01’, ‘2024-01-01’) |
Paso 3: Calcular las medias móviles a corto plazo (50 días) y a largo plazo (200 días)
| # Calculate short-term (fast) and long-term (slow) moving averages |
| aapl_data[‘SMA_50’] = aapl_data[‘Close’].rolling(window=50).mean() |
| aapl_data[‘SMA_200’] = aapl_data[‘Close’].rolling(window=200).mean() |
Paso 4: Generar señales basadas en el cruce de la media móvil
| # Generate signals based on moving average crossover |
| aapl_data[‘Signal’] = 0 # 0 indicates no signal |
| aapl_data.loc[aapl_data[‘SMA_50’] > aapl_data[‘SMA_200’], ‘Signal’] = 1 # 1 indicates buy signal |
| aapl_data.loc[aapl_data[‘SMA_50’] < aapl_data[‘SMA_200’], ‘Signal’] = –1 # -1 indicates sell signal |
Paso 5: Calcular los rendimientos diarios en función de las señales
| # Calculate daily returns based on signals |
| aapl_data[‘Daily_Return’] = aapl_data[‘Close’].pct_change() |
| aapl_data[‘Strategy_Return’] = aapl_data[‘Signal’].shift(1) * aapl_data[‘Daily_Return’] |
Paso 6: Calcular rendimientos acumulados
| # Calculate cumulative returns |
| aapl_data[‘Cumulative_Strategy_Return’] = (1 + aapl_data[‘Strategy_Return’]).cumprod() |
Paso 7: Imprima los rendimientos acumulados
| # Print the cumulative returns and plot the results |
| print(«Cumulative Strategy Return:») |
| print(aapl_data[‘Cumulative_Strategy_Return’].iloc[–1]) |
Salida:
Retorno de la estrategia acumulativa: 1.0439783521327737
Paso 8: Trazar las señales de la estrategia
| # Plotting the strategy signals |
| plt.figure(figsize=(12, 6)) |
| plt.plot(aapl_data[‘Close’], label=‘AAPL Close Price’, alpha=0.5) |
| plt.plot(aapl_data[‘SMA_50’], label=’50-day SMA’) |
| plt.plot(aapl_data[‘SMA_200’], label=‘200-day SMA’) |
| plt.plot(aapl_data.loc[aapl_data[‘Signal’] == 1, ‘Close’], ‘^’, markersize=3, color=‘g’, label=‘Buy Signal’) |
| plt.plot(aapl_data.loc[aapl_data[‘Signal’] == –1, ‘Close’], ‘v’, markersize=3, color=‘r’, label=‘Sell Signal’) |
| plt.title(‘AAPL Stock Price with Moving Average Strategy Signals’) |
| plt.xlabel(‘Date’) |
| plt.ylabel(‘Stock Price’) |
| plt.legend() |
| plt.show() |
Salida:
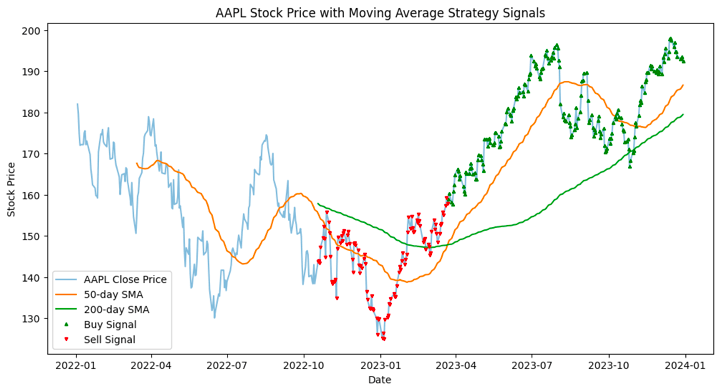
La figura trazada muestra el precio histórico de las acciones de AAPL junto con dos promedios móviles (50 días y 200 días) y las señales generadas por una estrategia simple de cruce de la media móvil.
Veamos el desglose de los componentes de la trama a continuación.
Línea de precios de cierre de AAPL:
La línea azul claro representa los precios de cierre diarios de AAPL durante el período especificado.
Línea de media móvil simple (SMA) de 50 días:
La línea naranja representa la SMA de 50 días de los precios de cierre de AAPL. Esta línea suaviza las fluctuaciones a corto plazo y proporciona una señal de seguimiento de tendencias.
Línea de media móvil simple (SMA) de 200 días:
La línea verde representa el SMA de 200 días de los precios de cierre de AAPL. Esta línea suaviza las fluctuaciones a largo plazo y proporciona una señal de seguimiento de tendencias a más largo plazo.
Comprar señales (Triángulo verde ‘^’):
Los triángulos verdes indican los puntos en los que la SMA de 50 días cruza por encima de la SMA de 200 días, generando una señal de compra. Este cruce se considera alcista en el análisis técnico.
Señales De Venta (triángulo Rojo Invertido ‘v’):
Los triángulos rojos invertidos indican los puntos en los que la SMA de 50 días cruza por debajo de la SMA de 200 días, generando una señal de venta. Este cruce se considera bajista en el análisis técnico.
Al observar las señales y las medias móviles, los operadores pueden potencialmente tomar decisiones sobre cuándo entrar o salir de posiciones en función de la estrategia.
Paso 9: Calcular el ratio Sharpe
| mean_strategy_return = aapl_data[‘Strategy_Return’].mean() |
| std_dev_strategy_return = aapl_data[‘Strategy_Return’].std(ddof=1) |
| # ddof=1 or Delta Degrees of Freedom for sample standard deviation |
| # Annual risk-free rate |
| annual_risk_free_rate = 0.05 |
| # Convert annual risk-free rate to daily rate |
| daily_risk_free_rate = annual_risk_free_rate / 252 |
| # Calculate Sharpe Ratio with daily risk-free rate |
| excess_return = aapl_data[‘Strategy_Return’] – daily_risk_free_rate |
| sharpe_ratio = np.sqrt(len(aapl_data)) * (mean_strategy_return / std_dev_strategy_return) |
| print(f»Sharpe Ratio with daily risk-free rate: {sharpe_ratio}«) |
Salida:
Ratio Sharpe para la estrategia: 0.2954069610097365
El Ratio Sharpe de 0,295 indica un rendimiento positivo ajustado por riesgo para la inversión o cartera en relación con una tasa libre de riesgo, lo que sugiere que la inversión ha proporcionado rendimientos que justifican el riesgo asumido.
En el código anterior, hemos asumido que la tasa de rendimiento sin riesgo es del 5 %, que se puede cambiar en consecuencia.
**Nota: El valor específico para la tasa libre de riesgo utilizada en el cálculo del Ratio Sharpe depende del marco de tiempo y de la moneda en la que se miden los rendimientos. Por lo general, se utiliza el rendimiento de los valores gubernamentales a corto plazo, como los bonos del Tesoro a 3 meses. **
Conceptos erróneos comunes sobre el ratio Sharpe
El ratio de Sharpe es una métrica ampliamente reconocida para evaluar el rendimiento ajustado al riesgo de las inversiones. Sin embargo, varios conceptos erróneos rodean su interpretación y aplicación.
Aquí hay algunos conceptos erróneos comunes sobre el ratio Sharpe:
- Medida absoluta del rendimiento: Una idea errónea común es ver el ratio de Sharpe como una medida absoluta del rendimiento. Si bien un Ratio de Sharpe más alto generalmente indica mejores rendimientos ajustados al riesgo, es esencial compararlo con puntos de referencia relevantes o grupos de pares para evaluar el rendimiento relativo con precisión.
- Énfasis excesivo en el valor numérico: algunos inversores pueden poner un énfasis excesivo en el logro de un objetivo específico de Ratio de Sharpe sin tener en cuenta la estrategia de inversión subyacente, las condiciones del mercado o los factores cualitativos. El contexto en el que se calcula el Ratio de Sharpe es crucial para su interpretación significativa.
- Suposición de la tasa libre de riesgo: Otra idea errónea es asumir una tasa libre de riesgo constante o universal para calcular el Ratio de Sharpe en diferentes mercados o períodos de tiempo. La elección de la tasa libre de riesgo debe ser apropiada y reflejar la moneda y la duración de la inversión.
- Sensibilidad a valores extremos: la relación de nitidez es sensible a los valores extremos o valores atípicos en los datos de retorno. Algunos inversores pueden malinterpretar una fuerte fluctuación en el Ratio de Sharpe debido a rendimientos extremos como un cambio significativo en el rendimiento ajustado al riesgo, mientras que podría ser una anomalía temporal causada por valores atípicos.
- Métrica de evaluación única del rendimiento: Si bien el Ratio de Sharpe es una métrica valiosa, confiar únicamente en ella para evaluar el rendimiento de la inversión puede ser limitante. La incorporación de otras métricas de rendimiento, el análisis cualitativo y la consideración del contexto de inversión más amplio proporciona una evaluación más completa.
- Inclusión del apalancamiento: al comparar los Ratios de Sharpe entre las inversiones, es esencial considerar si se utilizan el apalancamiento o los fondos prestados. Un ratio de Sharpe más alto como resultado del apalancamiento no puede indicar necesariamente una habilidad de inversión superior, sino más bien un aumento de la asunción de riesgos.
- Homogeneidad del riesgo: asumir que todas las inversiones tienen un perfil de riesgo similar o que el Ratio de Sharpe proporciona una representación completa de las características de riesgo de una inversión es una idea errónea. El Ratio de Sharpe se centra en la volatilidad medida por la desviación estándar, pero puede que no capture todos los aspectos del riesgo de una inversión, como el riesgo de liquidez o el riesgo geopolítico.
Limitaciones del Ratio Sharpe en el trading
El Ratio de Sharpe es una medida ampliamente utilizada para evaluar el rendimiento ajustado al riesgo de una inversión o cartera. Sin embargo, como cualquier métrica financiera, tiene sus limitaciones.
Aquí hay una tabla que resume algunas de las limitaciones clave de la proporción de Sharpe:
| limitación | descripción |
| Sensibilidad a la distribución de retorno | El Ratio de Sharpe asume que los rendimientos se distribuyen normalmente, pero los mercados financieros a menudo exhiben una no normalidad, con colas gordas y astisismos. En presencia de eventos extremos o valores atípicos, el Ratio de Sharpe puede no reflejar con precisión el riesgo asociado con la inversión. |
| Dependencia de datos históricos | El Ratio de Sharpe se basa en datos históricos, y el rendimiento pasado no garantiza resultados futuros. Los cambios en las condiciones del mercado, los factores económicos o el panorama de la inversión pueden conducir a diferentes perfiles de riesgo-rendimiento en el futuro. Los inversores deben tener cuidado cuando se basan únicamente en Ratio de Sharpe históricos para la toma de decisiones. |
| Métrica única para la comparación de carteras | Al comparar múltiples carteras o estrategias de inversión, es posible que el Ratio de Sharpe no proporcione una imagen completa. Se centra en los rendimientos ajustados al riesgo, pero no tiene en cuenta otros factores importantes como la exposición al mercado, el estilo o los aspectos cualitativos del proceso de inversión. Los inversores deben utilizar métricas y análisis adicionales para una evaluación exhaustiva de las opciones de inversión. |
| Sensibilidad a la elección de referencia | La elección de un índice de referencia para la comparación puede tener un impacto significativo en el Ratio de Sharpe. Los diferentes puntos de referencia pueden dar lugar a diferentes evaluaciones de rendimiento ajustadas al riesgo. Los inversores deben seleccionar cuidadosamente los puntos de referencia que sean relevantes para la estrategia y los objetivos de inversión. |
| Dependencia del período de tiempo | El Ratio de Sharpe puede variar dependiendo del período de tiempo elegido. Las fluctuaciones a corto plazo o las anomalías del mercado pueden tener un efecto más pronunciado en la proporción en plazos más cortos. Las perspectivas a largo plazo pueden proporcionar una evaluación más estable, pero podrían perderse los cambios recientes en la dinámica de riesgo-rendimiento. Los inversores deben considerar múltiples marcos de tiempo y analizar la coherencia del rendimiento. |
| Ignora las consideraciones no financieras | El Ratio de Sharpe se centra exclusivamente en las métricas de riesgo y rendimiento, descuidando factores no financieros como las consideraciones éticas, el impacto social y la gobernanza. Los inversores con criterios no financieros específicos pueden necesitar complementar el Ratio de Sharpe con otras métricas que aborden estos aspectos. |
| Asume una tasa constante sin riesgo | El Ratio de Sharpe asume una tasa constante sin riesgo a lo largo del tiempo. En realidad, la tasa libre de riesgo puede fluctuar, especialmente en respuesta a las condiciones económicas y las políticas del banco central. Los cambios en la tasa libre de riesgo pueden afectar a la interpretación del Ratio de Sharpe, particularmente cuando se compara el rendimiento en diferentes períodos de tiempo o entornos económicos. |
| Puede favorecer las estrategias con una ascación positiva | El Ratio de Sharpe penaliza las estrategias con una asisiación negativa, que puede no ser adecuada para todos los inversores. Algunos inversores pueden tolerar o incluso preferir la protección a la baja sobre el potencial al alza. El ratio de Sharpe no diferencia entre la volatilidad hacia arriba y hacia abajo, y las estrategias con asimetría positiva (asimetría favorable) pueden recibir ratios de Sharpe más altos incluso si no se alinean con las preferencias de riesgo de un inversor. |
¿Cómo mejorar el Ratio de Sharpe para nuestra estrategia?
Vemos algunos consejos que pueden ayudar a mejorar el Ratio de Sharpe de su estrategia.
Gestión de riesgos
- Implementar una estrategia sólida para limitar las pérdidas potenciales.
- Considere las órdenes de stop-loss, el tamaño de la posición basado en la volatilidad o la diversificación.
Costes de transacción
- Tenga en cuenta los costos de transacción y el deslizamiento en su estrategia.
- Optimizar la ejecución de operaciones para minimizar los costos.
Optimizar los parámetros
Ajuste los parámetros de la estrategia (por ejemplo, longitudes de la media móvil) para obtener rendimientos máximos ajustados por riesgo.
Incluir los costos de transacción en la prueba posterior
Asegúrese de que las pruebas adicionales tengan en cuenta los costos de transacción realistas para reflejar las condiciones de mercadoc del mundo real.
Preguntas frecuentes sobre el Ratio de Sharpe
Estas son algunas de las preguntas más frecuentes sobre el Ratio de Sharpe:
P. ¿Cuáles son algunas ideas a tener en cuenta al calcular el Ratio de Sharpe?
R: Aquí puede ver algunas de las mejores ideas según la experiencia de algunos traders profesionales:
- Período de tiempo consistente: Asegúrese de que los datos de retorno y la tasa libre de riesgo sean consistentes y estén alineados para el período de tiempo elegido.
- Tasa libre de riesgo precisa: Utilice una tasa libre de riesgo adecuada que coincida con la moneda y la duración de la inversión.
- Manejo robusto de datos: Maneje valores atípicos o valores extremos en los datos de retorno de manera adecuada para evitar la distorsión en el cálculo del Ratio de Sharpe.
- Comparación de puntos de referencia: Considere la posibilidad de comparar el ratio de Sharpe calculado con puntos de referencia o grupos de pares relevantes para el contexto y la evaluación del rendimiento relativo.
P. ¿Qué se entiende por Ratio de Sharpe en la teoría moderna de carteras?
R: El Sharpe Ratio juega un papel crucial en la Teoría Moderna de Carteras (MPT) al ayudar a los inversores a construir carteras eficientes que maximicen los rendimientos para un nivel de riesgo determinado. MPT hace hincapié en la diversificación y en los beneficios de combinar activos con diferentes perfiles de riesgo-rendimiento para lograr una asignación óptima de la cartera.
P. ¿Cuál es el impacto del ratio de Sharpe en la estrategia de inversión?
R: El Ratio de Sharpe influye en la estrategia de inversión al guiar las decisiones sobre la asignación de activos, la gestión de riesgos y la evaluación del rendimiento. Una comprensión profunda del Ratio de Sharpe ayuda a los inversores a optimizar sus carteras, alinear las inversiones con sus objetivos de tolerancia al riesgo y rendimiento y, en última instancia, mejorar los resultados de la inversión a largo plazo.
P: ¿Qué es un buen Ratio de Sharpe?
R: Un buen ratio de Sharpe indica rendimientos superiores ajustados por riesgo, generalmente por encima de 1. Por ejemplo, 1,5 significa que su exceso de rendimiento sobre la tasa libre de riesgo es 1,5 veces la volatilidad de su cartera.
P: ¿Qué es un alto Ratio de Sharpe?
R: Un altor ratio de Sharpe significa un rendimiento excepcional, que normalmente supera los 2. Esto sugiere que su cartera genera rendimientos significativamente más altos en comparación con su nivel de riesgo.
P: ¿Qué es un Ratio de Sharpe negativo?
R: El ratio de Sharpe negativo significa que su cartera sufre pérdidas que superan la tasa libre de riesgo. Esto implica que las inversiones elegidas tienen un rendimiento inferior incluso en comparación con una opción segura como los bonos del gobierno.
P: ¿Qué es un ratio de Sharpe condicional?
R: El ratio de Sharpe condicional mide los rendimientos ajustados al riesgo en condiciones específicas del mercado, como el aumento o la caída de las tasas de interés. Ayuda a evaluar el rendimiento de su cartera en diferentes escenarios.
Conclusión
El Ratio de Sharpe, una métrica fundamental en las finanzas, mide el rendimiento ajustado al riesgo de una inversión, ayudando en la evaluación de la cartera, la gestión del riesgo y la creación de estrategias. Desarrollado por William F. Sharpe compara el exceso de rendimiento de un activo con su volatilidad, con valores más altos que indican un rendimiento superior ajustado al riesgo.
Sin embargo, existen conceptos erróneos y limitaciones, lo que requiere un enfoque matizado. Al integrar el Ratio de Sharpe con otras métricas y mejores prácticas, los inversores pueden optimizar el rendimiento de la cartera, alineándose con los principios de la Teoría Moderna de Carteras y mejorando las estrategias de inversión para el éxito a largo plazo.
