
El objetivo de Quantinsti es formar a su alumnos en el trading algorítmico. Pertenece a iRageCapital Advisory, empresa conocida por sus servicios relacionados con la creación de mesas de trading algorítmico.
Redes Neuronales en Python
Esta segunda parte de Redes Neuronales en Python incluye los siguientes tópicos:
- ¿Cómo entrenar una red neuronal?
- Función de costo
- Descenso del Gradiente
- Tipos de Descenso del Gradiente
- Retropropagación
¿Cómo entrenar una red neuronal?
Para simplificar las cosas en el tutorial de redes neuronales, podemos decir que existen dos formas de programar para realizar una tarea específica:
1. Todas las reglas del programa se definen, y se le dan las entradas para que compute el resultado.
2. Desarrollar un marco sobre el cual el código aprenderá a realizar la tarea específica entrenándose en un conjunto de datos y ajustando el resultado que calcula para que esté lo más cerca posible de los resultados reales observados.
Este segundo proceso se llama entrenar el modelo, que es en lo que nos vamos a enfocar. Veamos cómo nuestra red neuronal se entrenará para predecir los precios de las acciones.
La red neuronal recibirá el conjunto de datos, que consiste en los datos OHLCV (apertura, máximo, mínimo, cierre y volumen) como entrada. Como salida, también le daremos al modelo el precio de cierre del día siguiente, que es el valor que queremos que el modelo aprenda a predecir. El valor real de la salida será representado por ‘y’, y el valor predicho será representado por y^ (y sombrero).
El entrenamiento del modelo implica ajustar los pesos de las variables para todas las diferentes neuronas presentes en la red neuronal. Esto se realiza minimizando la Función de Costo. La función de costo, como su nombre lo indica, es el costo de hacer una predicción usando la red neuronal. Es una medida de cuán alejado está el valor predicho, y^, del valor real u observado, y.
Existen muchas funciones de costo utilizadas en la práctica, pero la más popular se calcula como la mitad de la suma de las diferencias al cuadrado entre los valores reales y los predichos para el conjunto de entrenamiento:
C = \(\sum \frac{1}{2} (y^ – y)^2 \)
Primero, la red neuronal se entrena calculando la función de costo para el conjunto de entrenamiento. Es importante destacar que el conjunto de entrenamiento tiene un conjunto inicial de pesos para las neuronas. Después, la red intenta mejorar ajustando esos pesos.
Luego, la red neuronal recalcula la función de costo con los nuevos pesos. Este proceso completo de corrección de errores y ajuste de pesos después de las correcciones se llama retropropagación.
El objetivo es minimizar la función de costo, y la retropropagación se repite hasta que se minimiza. Durante este proceso, también se ajustan los pesos.
Una manera de hacerlo sería mediante fuerza bruta. Supongamos que hay 1000 valores posibles para los pesos. Ahora, evaluaremos la función de costo con estos 1000 valores.
El gráfico de la función de costo se vería como el siguiente:
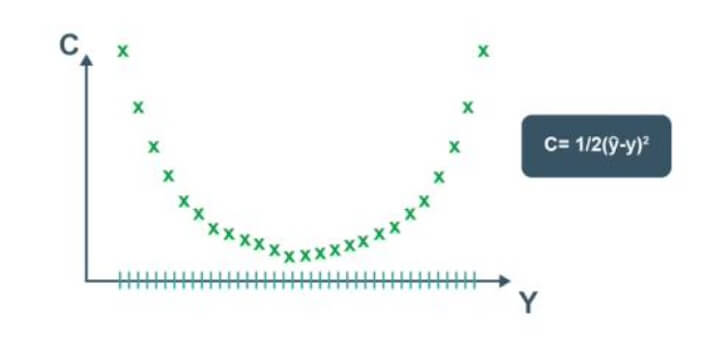
Función de costo
Este enfoque podría funcionar para una red neuronal con un solo peso que debe optimizarse. Sin embargo, a medida que aumenta el número de pesos y el número de capas ocultas, el número de cálculos necesarios también aumenta drásticamente.
El tiempo necesario para entrenar un modelo así sería extremadamente largo, incluso en la supercomputadora más rápida del mundo. Por esta razón, es fundamental desarrollar una metodología más rápida y eficiente para calcular los pesos de la red neuronal. Este proceso se llama Descenso de Gradiente.
Descenso del Gradiente
El descenso del gradiente analiza la función de costo y muestra, a través de la pendiente de la curva (como se ve en la imagen a continuación), cómo ajustar los pesos. Esto ayuda a minimizar la función de costo.
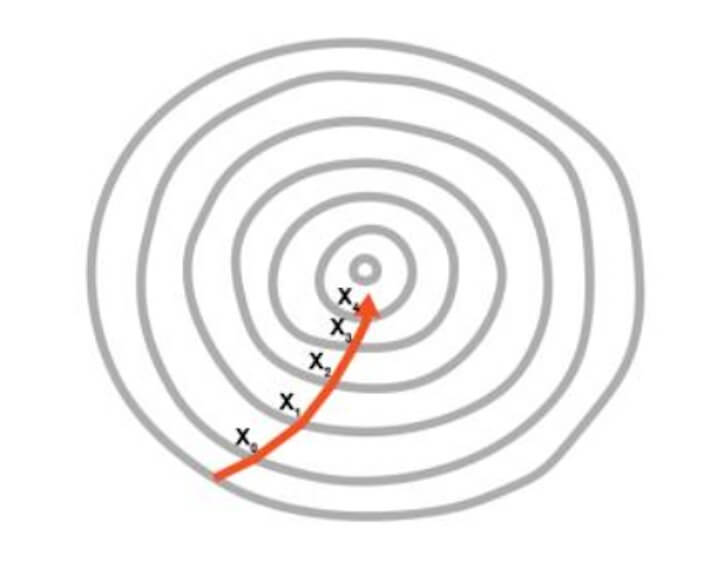
La visualización del descenso del gradiente se muestra en los diagramas siguientes. El primer gráfico es bidimensional. La imagen muestra un círculo rojo que se mueve en un patrón de zigzag hasta alcanzar finalmente la función de costo mínima.
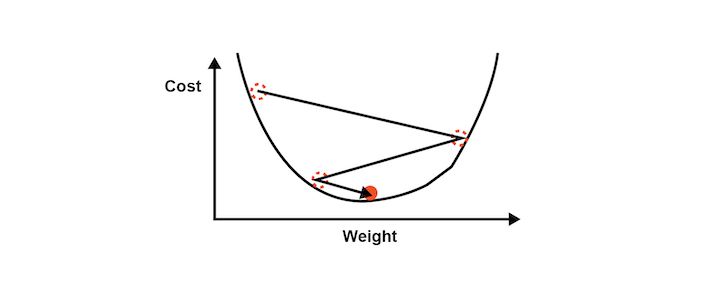
En la segunda imagen, es necesario ajustar dos pesos para minimizar la función de costo.
Por lo tanto, se puede ver como un contorno en la imagen, donde la dirección es hacia la pendiente más pronunciada y se busca llegar al mínimo en el menor tiempo posible. Este enfoque no requiere muchos procesos computacionales y tampoco es extremadamente largo. Se puede decir que entrenar el modelo es una tarea factible.
Tipos de Descenso del Gradiente
El descenso de gradiente se puede realizar de tres maneras posibles:
1. Descenso del Gradiente por Lotes
En este tipo, la función de costo se calcula sumando todas las funciones de costo individuales en el conjunto de entrenamiento. Después de este paso, se calcula la pendiente ajustando los pesos del conjunto de datos de entrenamiento.
2. Descenso del Gradiente Estocástico
En este tipo de descenso del gradiente, cada entrada de datos es seguida por la creación de la pendiente de la función de costo y el ajuste de los pesos en el conjunto de datos de entrenamiento. Esto ayuda a evitar los mínimos locales si la curva de la función de costo no es convexa.
Además, cada vez que se ejecuta el proceso de descenso del gradiente estocástico, el camino hacia el mínimo puede ser diferente.
3. Descenso del Gradiente en Mini Lotes
El tercer tipo es el descenso del gradiente en mini lotes, que es una combinación de los métodos por lotes y estocástico. Aquí se crean diferentes lotes agrupando varias entradas de datos en un solo lote. Esto resulta en la implementación del descenso del gradiente estocástico sobre lotes más grandes de entradas en el conjunto de entrenamiento.
Retropropagación
La retropropagación es un algoritmo avanzado que nos permite actualizar todos los pesos en la red neuronal de manera simultánea. Esto reduce drásticamente la complejidad del proceso de ajuste de pesos. Si no usáramos este algoritmo, tendríamos que ajustar cada peso individualmente, determinando el impacto que ese peso tiene en el error de la predicción.
Pasos del Entrenamiento con Descenso de Gradiente Estocástico:
1. Inicializar los pesos a valores pequeños, muy cercanos a 0 (pero no 0).
2. Propagación hacia adelante: Las neuronas se activan de izquierda a derecha usando la primera entrada de datos de nuestro conjunto de entrenamiento hasta llegar al resultado predicho, y.
3. Cálculo del error: Se mide el error generado.
4. Retropropagación: El error generado se retropropaga de derecha a izquierda, ajustando los pesos según la tasa de aprendizaje.
5. Repetir los pasos de propagación hacia adelante, cálculo del error y retropropagación en todo el conjunto de entrenamiento.
6. Fin de la primera época: Las épocas sucesivas comenzarán con los valores de los pesos de la época anterior. Este proceso se puede detener cuando la función de costo alcanza un límite aceptable.
