![]()
Niels Bohr, el premio Nobel de Física, dijo: «La predicción es muy difícil, especialmente si se trata del futuro». En el ámbito del análisis financiero, estimar los rendimientos a largo plazo de las acciones en un horizonte de 10 a 20 años presenta un desafío increíble. A pesar de los desafíos significativos en la previsión de las tendencias del mercado y las condiciones económicas durante períodos tan largos, esta tarea sigue siendo importante para los inversores, los gestores de carteras y los responsables políticos, ya que algunos de ellos a menudo dependen de estas previsiones para desarrollar estrategias de inversión y marcos de políticas eficaces. La información del documento revisado de hoy da información valiosa sobre cómo mejorar estas predicciones.
El documento, llamado, título traducido al español, Estimación de los rendimientos esperados a largo plazo, trata de estimar con precisión los rendimientos esperados a largo plazo de los mercados de valores, lo que es esencial para las entidades corporativas y los inversores individuales de la misma manera. Investigan la capacidad de diferentes marcos y proxies de entrada para estimar los rendimientos de OOS a 10 y 20 años durante largos períodos de tiempo históricos y períodos más recientes. Descubrieron que varios enfoques generan mejoras significativas en comparación con las previsiones históricas del modelo medio. OOS-R2 puede ser tan significativo como el 40 % incluso en el período más reciente, y la asignación de activos basada en las previsiones del modelo presentado puede mejorar la relación Sharpe y el VaR de una cartera en más del 50 %.
Las metodologías que los autores emprendieron consisten en ejecutar varios marcos y proxies utilizados para generar pronósticos E(R) a largo plazo y comparar el rendimiento de los enfoques para estimar los rendimientos esperados que se han considerado principalmente de forma aislada. Muestran que los E(R) a 10 a 20 años se pueden estimar ex-ante: las mejoras en el pronóstico fuera de la muestra (OOS) sobre los pronósticos medios históricos son tan grandes como el 40 %, incluso en el período más reciente. Es importante destacar que estas ganancias existen dentro de un rango de períodos de tiempo.
Los resultados son de interés para aquellos que requieren pronósticos de retorno precisos a largo plazo, y alentamos especialmente a los lectores ávidos a que miren las Tablas 1 y 2, que proporcionan resúmenes perspicaces de los hallazgos críticos del documento.
- Autores: Rui Ma, Ben R. Marshall, Nhut H. Nguyen, Nuttawat Visaltanachoti
- Título: Estimating Long-Term Expected Returns (Estimación de los rendimientos esperados a largo plazo)
- Enlace: https://papers.ssrn.com/sol3/papers.cfm? abstract_id=4493448
Resumen
Es de vital importancia es estimar los rendimientos esperados a largo plazo con la mayor precisión posible. Los investigadores suelen basar sus estimaciones en el rendimiento y el crecimiento, la valoración o un marco combinado de rendimiento, crecimiento y valoración. Nuestros resultados indican que varios enfoques superan en gran medida las estimaciones basadas en rendimientos medios históricos del punto de referencia, con mejoras en el error cuadrado medio que superan el 40 %. El uso de estos enfoques en las decisiones de asignación de activos da como resultado una mejora en los ratios de Sharpe de más del 50 %.
Como siempre, presentamos varias figuras y tablas interesantes:
Citas notables del trabajo de investigación académica:
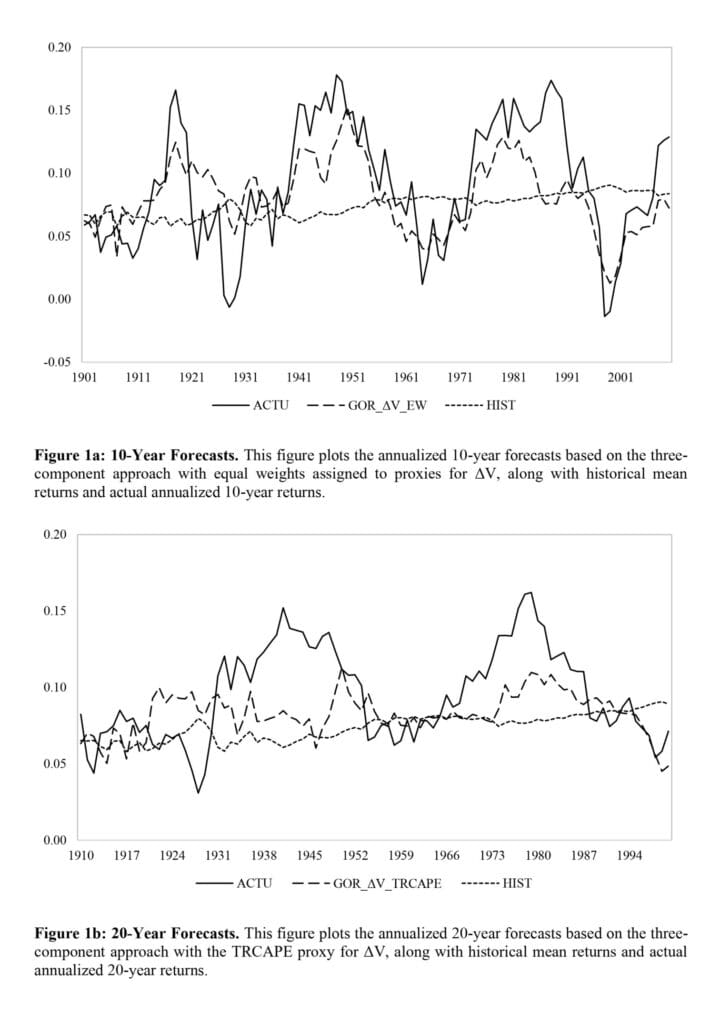
«Nuestros resultados indican que el marco de tres componentes es superior para las previsiones de 10 años, aunque no por un gran margen. El modelo de tres componentes que genera estimaciones de ΔV basadas en la composición de la cartera de riqueza de Rintamaki (2023), denotado como VWPC, supera a otros modelos de tres componentes en la previsión de rendimientos a 10 años para todo el período de muestra de 1891 a 2020. Sin embargo, en dos períodos de submuestra más recientes, no es estadísticamente diferente de otros modelos de tres componentes, como el que asigna un peso igual a cuatro proxies para ΔV. Sugerimos que este último modelo es superior en general, ya que funciona mejor en un entorno de asignación de activos. Genera una reducción del 34,91 % en los MAE y un aumento del 57,70 % en el OOS-R2 en comparación con el modelo medio histórico para las previsiones de 10 años durante el período de muestra de 1891-2020. Además, una cartera de bonos de acciones con pesos asignados en base a estas previsiones de E(R) tiene un ratio Sharpe aproximadamente un 65,56 % más alto y una mejora del 50,06 % en el valor en riesgo (VaR) durante el período 1891-2020. Es importante destacar que este modelo también conduce a ganancias de mejora en períodos más recientes. Los rendimientos a veinte años suelen ser más difíciles de predecir. Sin embargo, varios enfoques, como el modelo de tres componentes con el proxy de la relación precio/beneficio (TRCAPE) de rendimiento total ajustado cíclicamente, mejoran significativamente la precisión de estas predicciones.»
«Contribuimos a varias líneas de los estudios publicados sobre la previsibilidad del retorno a largo plazo. Fama y French (1988) utilizan un enfoque de rendimiento solo y muestran que los rendimientos de dividendos explican más del 25% de la variación de los rendimientos de dos a cuatro años. Campbell y Shiller (1998) contribuyen a la literatura de la valoración sola al centrarse en predecir los rendimientos a 10 años utilizando una relación precio/ganancias que se deriva de las ganancias promedio de los últimos 10 años. Sugieren que la contabilidad de las fluctuaciones de las ganancias a lo largo del ciclo económico es importante y muestran que esta métrica, que se conoce ampliamente como la relación precio/ganancias ajustada cíclicamente (CAPE), es efectiva para predecir los rendimientos de las acciones. Bogle (1991a, b) introduce el enfoque de tres componentes y sugiere que las previsiones de los rendimientos a 10 años dan «una replicación notablemente precisa de los rendimientos totales reales realizados».
«Presentamos estadísticas resumidas en la Tabla 1. Los rendimientos anuales promedio son del 10,66 %, 11,76 % y 12,27 % para los períodos de 1872-2020, 1955-2020 y 1988-2020, respectivamente. Los rendimientos tienen una astisidad negativa en los tres períodos de muestra. La kurtosis es negativa durante todo el período, pero positiva en los períodos más recientes. En el Panel B, presentamos rendimientos geométricos y de registro medios para intervalos de 10 y 20 años que avanzan un año a la vez. Son estos rendimientos de registro anualizados los que utilizamos en nuestros pronósticos de modelos. Para el intervalo de 10 años, los rendimientos de registro anualizados promedio son del 8,65 %, 9,40 % y 8,57 % para los tres períodos, respectivamente, mientras que para el intervalo de 20 años, estos son del 8,73 %, 9,68 % y 7,55 %, respectivamente. Del mismo modo, el Panel C informa de la desviación estándar de los rendimientos geométricos y los rendimientos para los intervalos de 10 y 20 años que se avanzan un año a la vez.»
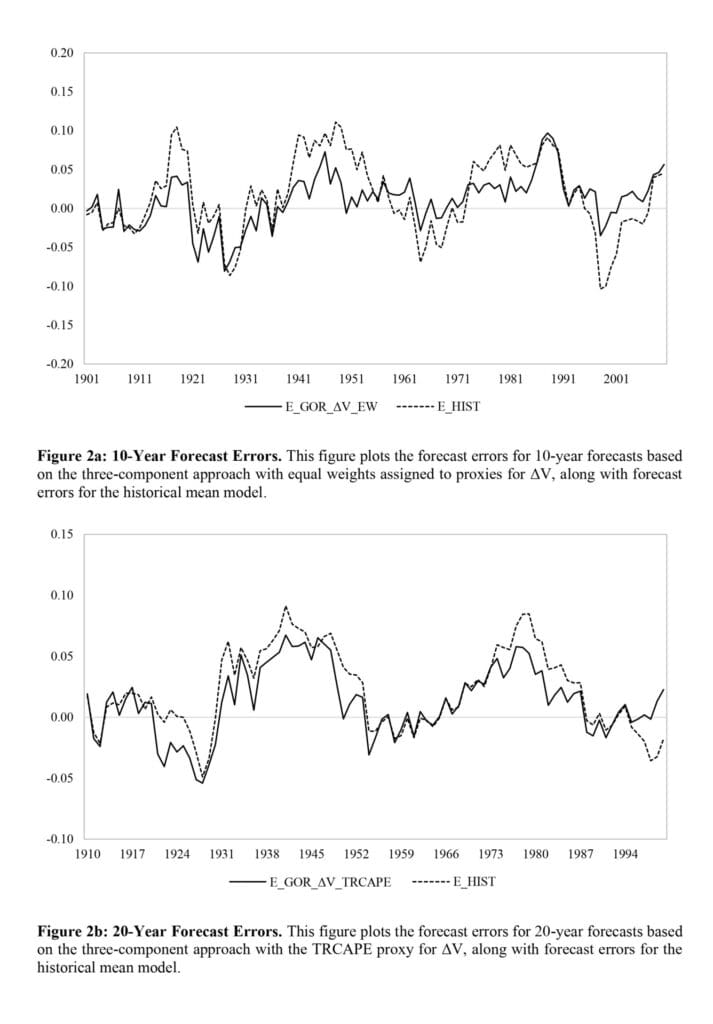
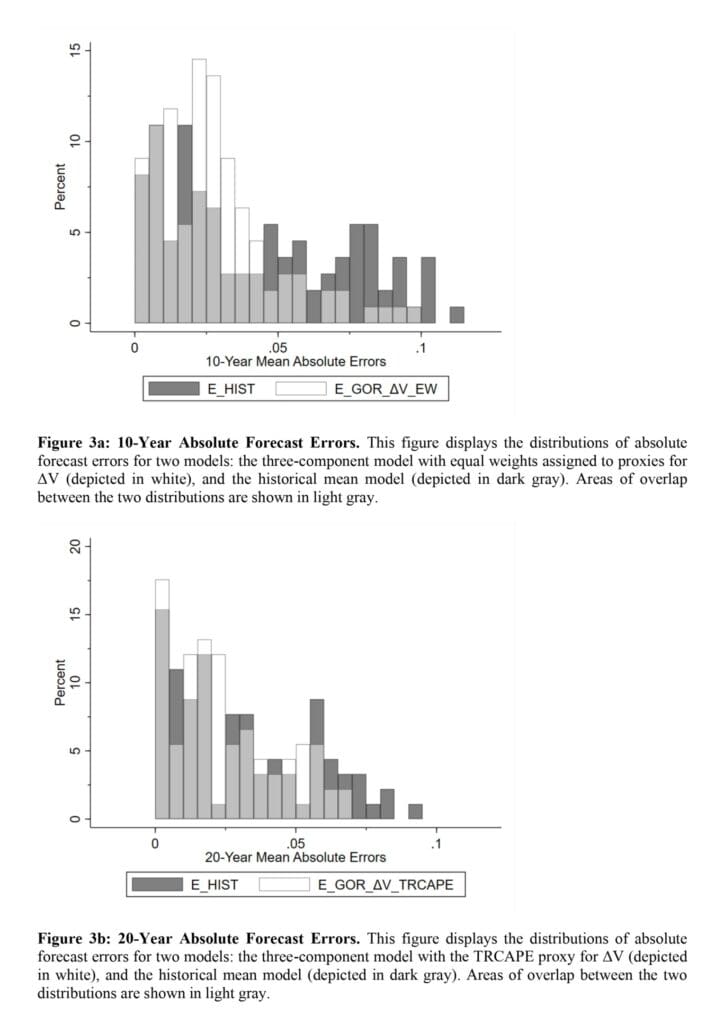
«En la Tabla 2, informamos de los resultados de los pronósticos de 10 años. Calculamos el MAE como la diferencia absoluta promedio entre el pronóstico y los rendimientos reales. También calculamos la diferencia en MAE entre cada modelo de predicción y el pronóstico medio histórico.7 Medimos la significación estadística de esta diferencia utilizando el método de arranque de bloques móviles, que tiene en cuenta la autocorrelación en la serie temporal. La longitud óptima del bloque se determina según Patton, Politis y White (2009). Para cada modelo de predicción, generamos 1000 remuestras de arranque e informamos de significación estadística basada en el valor p de arranque unilateral (es decir, la proporción de los MAE del modelo de predicción de muestra de arranque que exceden el modelo medio histórico MAE en la misma muestra de arranque).»
«Los resultados de la Tabla 2 indican que el marco de tres componentes es el marco de mejor rendimiento. Para las previsiones a 10 años, este marco tiene el promedio de MAE más bajo en los períodos de 1981-2020, 1955-2020 y 1988-2020. Para determinar la diferencia estadística entre el marco de «tres componentes» y los otros tres marcos (es decir, «rendimiento solo», «Gordon» y «valoración solo»), primero calculamos el error absoluto promedio anual para cada marco a lo largo del tiempo. Utilizando las cuatro series temporales resultantes, luego aplicamos la prueba Diebold-Mariano (Diebold y Mariano, 1995). Como se muestra en el Apéndice 3, el error absoluto promedio de «tres componentes» es estadísticamente significativamente menor que «Gordon» en los tres períodos de tiempo y estadísticamente significativamente más bajo que «valoración sola» y «rendimiento solo» en dos de los tres períodos de tiempo».
