![]()
El método de Monte Carlo (simulaciones de Monte Carlo) es una clase de algoritmos que se basan en un muestreo aleatorio repetido para obtener resultados de varios escenarios. Las simulaciones de Monte Carlo se utilizan para predecir la probabilidad de diferentes resultados cuando sería difícil utilizar otros enfoques, como la optimización. El objetivo principal es crear escenarios alternativos, que den cuenta de los posibles riesgos y ayuden a la toma de decisiones. Las simulaciones se utilizan en varios campos, desde las finanzas y el análisis cuantitativo hasta la ingeniería o la ciencia. Planeamos presentar nuestro nuevo informe «Monte Carlo» para los clientes de Quantpedia Pro en los próximos días, y este artículo es nuestra introducción a las diferentes metodologías que se pueden usar para el cálculo de Monte Carlo.
Las simulaciones de Monte Carlo son una herramienta útil tanto para la gestión de riesgos como para la gestión de carteras. Los gestores de riesgos pueden calcular un presupuesto adecuado para una posible estrategia de inversión cuantitativa, mientras que los gestores de cartera pueden establecer sus expectativas con mayor precisión y realizar fácilmente un análisis de sensibilidad de sus estrategias. Las simulaciones de Monte Carlo son una opción para crear un sinfín de escenarios alternativos en los que probar tus estrategias. Su principal ventaja es que van más allá de los datos históricos y más bien alteran la historia de forma artificial.
Estrategia subyacente
En nuestro análisis, aplicamos simulaciones Monte Carlo a una estrategia de inversión cuantitativa. Más específicamente, utilizamos una estrategia de trading denominada factor de inversión de asimetría de retorno en futuros de materias primas . La estrategia se basa en la idea de que a mayor (menor) asimetría alcista se asocia una menor (mayor) rentabilidad esperada, analizada en numerosos estudios teóricos.
La estrategia de futuros de materias primas de Quantpedia tiene como objetivo examinar la asimetría de rendimiento en los futuros de materias primas de una manera un poco menos tradicional. En lugar de utilizar la asimetría como indicador de la asimetría de retorno, nos basamos en una nueva medida asimétrica IE propuesta por Jiang et al. (2020), que utiliza la diferencia entre las probabilidades de retorno al alza y a la baja para aprovechar el grado de asimetría.
En cuanto al universo de inversión, la estrategia sigue a Padyšák y Vojtko (2019). Su conjunto de datos de materias primas ofrece una amplia exposición al mercado de materias primas. La cartera se construye sobre la medida asimétrica de la siguiente manera. Al comienzo de cada mes, la asimetría de cada producto (IE) se calcula utilizando los últimos 260 rendimientos diarios. Después, las materias primas se clasifican de acuerdo con su IE. La cartera se coloca en largo en las cuatro materias primas inferiores con el IE más bajo en el mes anterior y en corto en las cuatro materias primas principales con el IE más alto en el último mes (los empates en los rangos pueden cambiar esto).
Tipos de simulación de estrategia de Monte Carlo
Hay varios tipos de aplicaciones de Monte Carlo en estrategias de trading cuantitativas. Nos centraremos en las diferentes formas de aleatorizar los rendimientos de la estrategia. En este artículo cubrimos los más prácticos y más utilizados:
- Muestreo de Monte Carlo sin reemplazo
- Muestreo de Monte Carlo con reemplazo
- Alteraciones de retorno de Monte Carlo
- Comparación con estrategias aleatorias
Ahora, podemos (y lo hacemos) aplicar cada uno de estos a:
- Rentabilidades periódicas de la estrategia (p. ej., rentabilidades mensuales) o
- Retorno comercial de la estrategia
Con rendimientos de período es más un enfoque de serie de tiempo, mientras que con rendimientos es más un punto de vista clásico de P&L de negociación.
Análisis
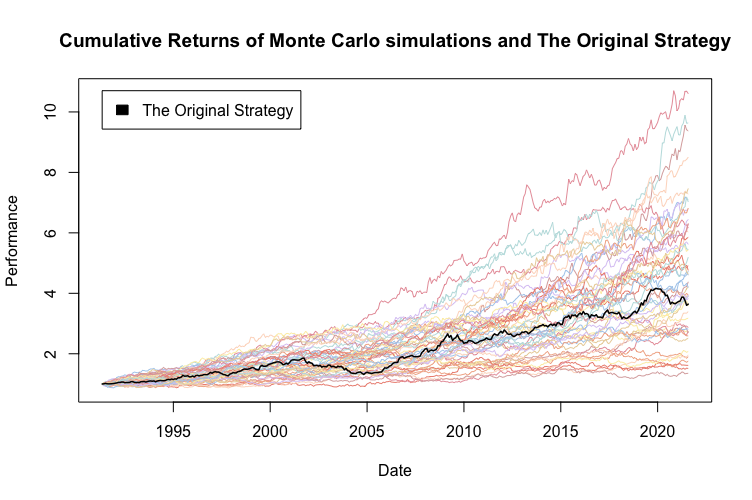
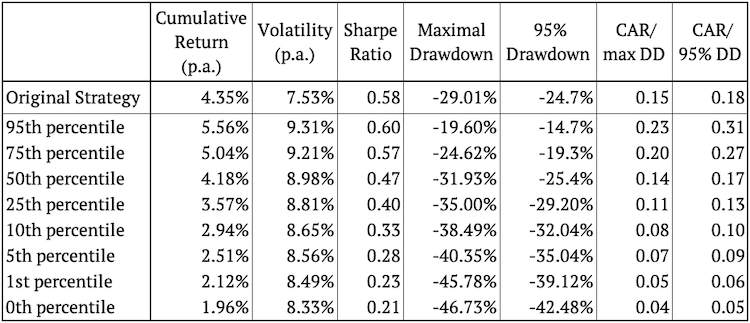
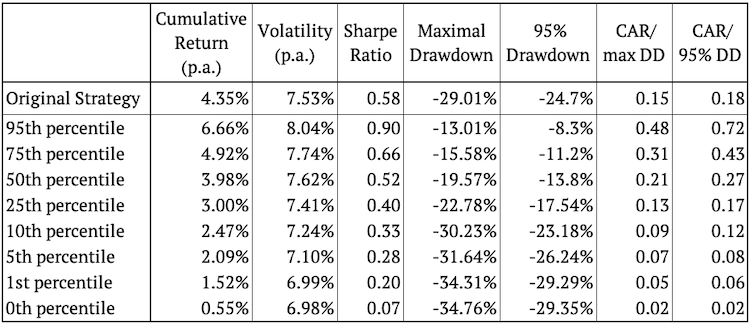
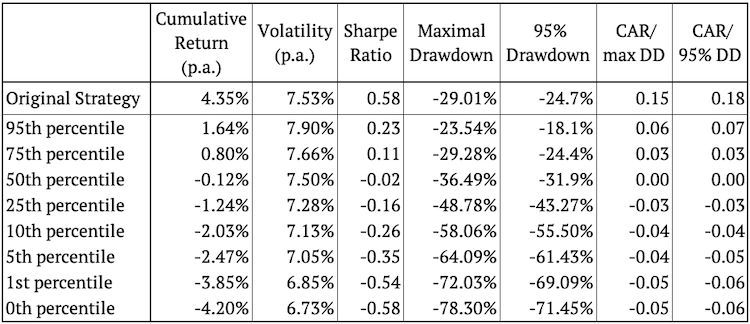
Como ya mencionamos, aplicamos simulaciones de Monte Carlo a una estrategia ya existente. La siguiente figura muestra el rendimiento acumulado de la estrategia original inalterada y también sus características de riesgo y rentabilidad.
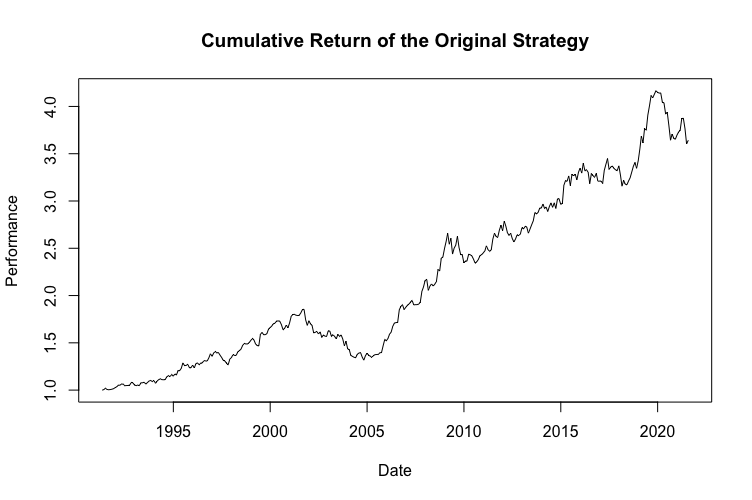

Nuestro análisis consta de tres partes, cada una de las cuales incluye múltiples enfoques para las simulaciones de Monte Carlo:
- La primera parte analiza los rendimientos mensuales de la estrategia y aplica los tres primeros métodos Monte Carlo mencionados anteriormente.
- La segunda parte hace lo mismo, pero utilizando devoluciones comerciales.
- Finalmente, la tercera parte presenta la comparación de la estrategia original contra estrategias aleatorias
Simulaciones de Monte Carlo de los rendimientos mensuales de la estrategia
En la primera sección, analizamos los rendimientos mensuales de la estrategia subyacente. En primer lugar, creamos un vector de rendimientos mensuales. Luego tomamos tres enfoques de las simulaciones de Monte Carlo para crear nuevos vectores.
Muestreo de Monte Carlo sin reemplazo
Este método de Monte Carlo solo cambia el orden de las rentabilidades, es decir, “reorganiza” las rentabilidades. La suposición principal detrás de este método es que los rendimientos permanecerán iguales (o similares) pero su orden de ocurrencia puede cambiar.
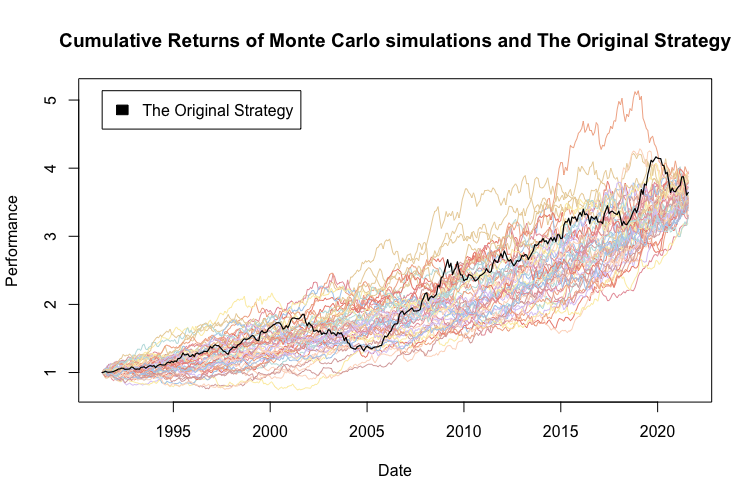
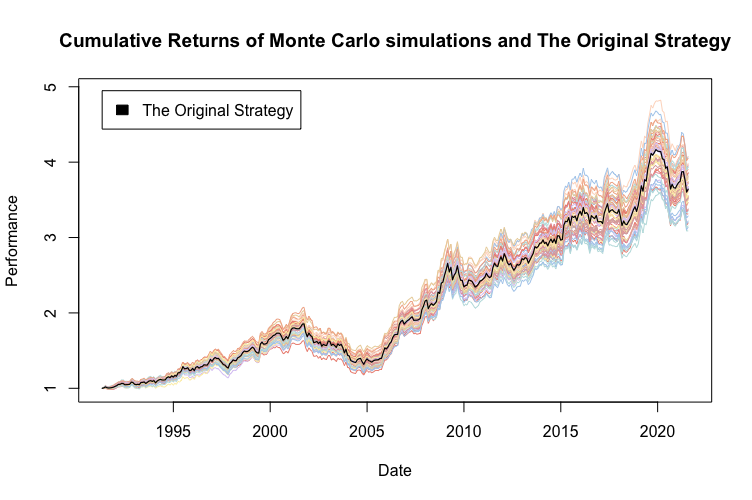
Técnicamente estamos hablando de un muestreo aleatorio simple sin reemplazo (reorganización de los datos). Creamos 100 nuevas muestras de la misma longitud aplicando aleatorización sin reemplazo. Básicamente, reorganizamos los datos 100 veces para crear 100 vectores nuevos y calculamos los rendimientos acumulativos de las estrategias simuladas. Para una mejor claridad visual, la siguiente figura muestra solo 50 de las 100 simulaciones.
Al utilizar el muestreo aleatorio de Monte Carlo sin reemplazo, la volatilidad de las estrategias simuladas será siempre la misma que la de la estrategia original. Además, el rendimiento acumulado será lógicamente muy similar, porque solo cambiamos el orden de los rendimientos y la única forma en que el rendimiento puede diferir es debido a la capitalización. El atributo más interesante de observar en este método de Monte Carlo es la reducción. El drawdown puede cambiar (y también cambia en nuestro caso) significativamente cuando cambiamos el orden de los rendimientos.
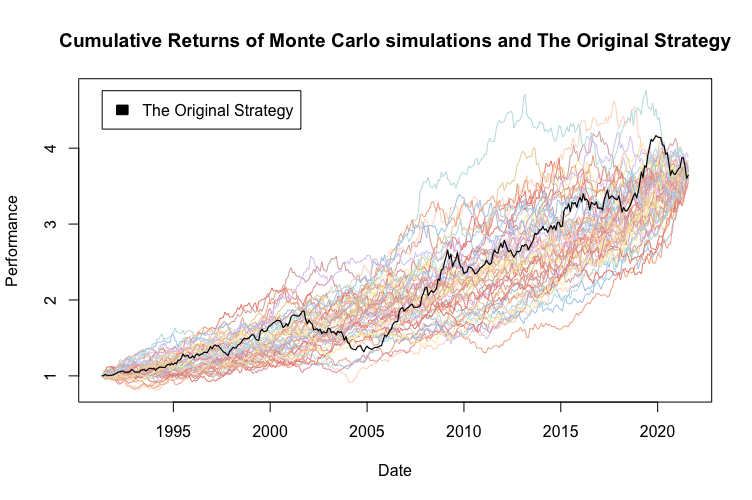
La figura anterior presenta varias realizaciones aleatorias de reorganización de órdenes de rentabilidad. La figura también muestra que la estrategia original se encuentra aproximadamente en el medio de las estrategias simuladas la mayor parte del tiempo, exactamente como se esperaba. Calculamos los percentiles 95, 75, 50, 25, 10, 5, 1 y 0 de la característica de riesgo y rendimiento para ver exactamente qué tan bien se desempeña en comparación con las simulaciones.
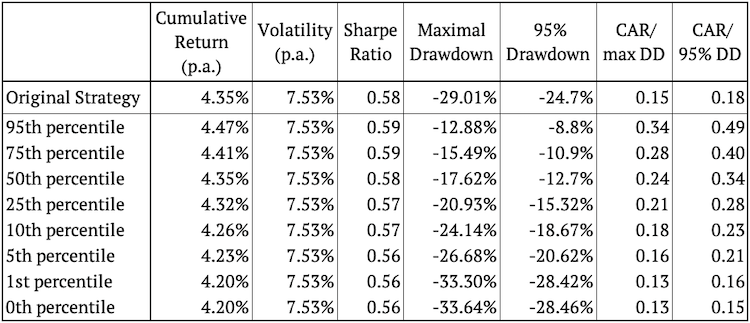
Curiosamente, más del 95% de las realizaciones aleatorias tienen una cifra de drawdown más baja (mejor) que la estrategia original. Esto sugiere que el drawdown de la estrategia original puede ser una cifra un poco conservadora.
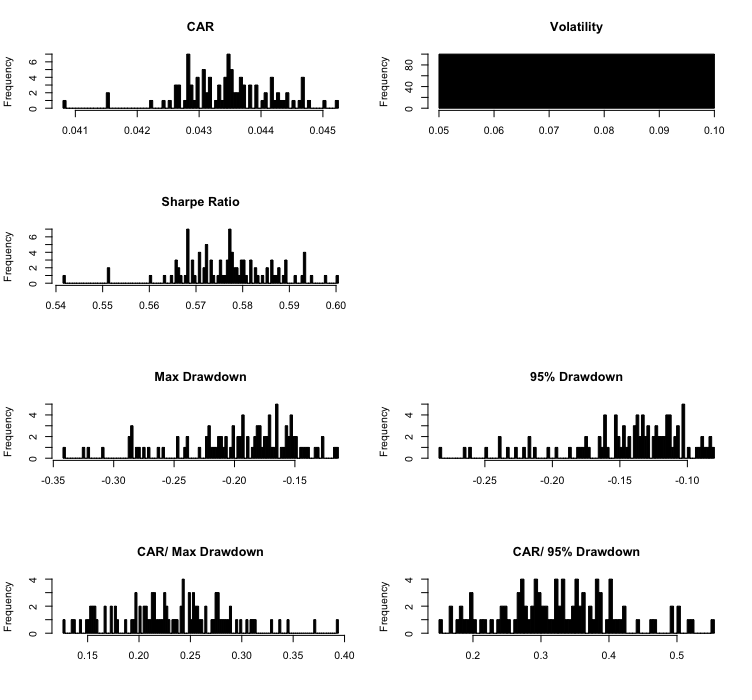
Además, la siguiente figura presenta un conjunto de histogramas que muestran la frecuencia de las características individuales de riesgo y rendimiento en nuestras 100 simulaciones. Solo hay un valor único para la volatilidad porque aplicamos el muestreo aleatorio sin reemplazo.
Muestreo de Monte Carlo con reemplazo
Este método de Monte Carlo no solo cambia el orden de las rentabilidades, sino que también omite o repite aleatoriamente las rentabilidades de la estrategia original. La suposición principal detrás de este método es que la distribución de la rentabilidad permanecerá igual (o similar), pero la rentabilidad puede cambiar de manera más significativa.
Técnicamente, estamos hablando de un muestreo aleatorio con reemplazo. Creamos 100 nuevas muestras de la misma longitud que el vector original de retornos aplicando aleatorización de retornos con reemplazo. Luego calculamos los rendimientos acumulados de las estrategias simuladas. Para mayor claridad, la siguiente figura muestra nuevamente solo 50 de las 100 simulaciones.
El muestreo de Monte Carlo con reemplazo crea mucha más variedad en los retornos de estrategias simuladas. Es lógico que la aleatorización con reemplazo pueda dar lugar a la repetición de varios meses sin éxito, así como a varios meses con éxito seguidos. Con este método también simulamos cambios en la volatilidad y en los rendimientos acumulados.
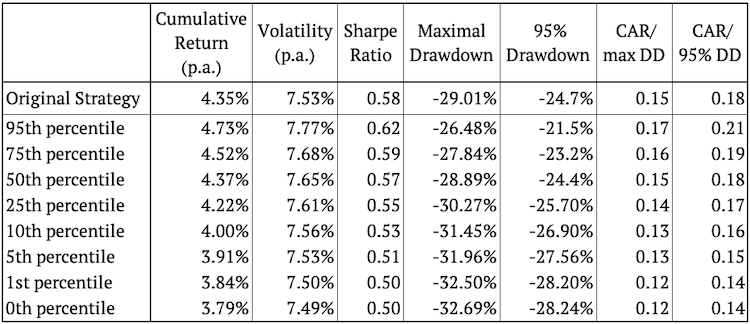
Una vez más, como era de esperar, la mayor parte del tiempo la estrategia original parece estar en medio de las estrategias simuladas. Nuevamente, calculamos los percentiles 95, 75, 50, 25, 10, 5, 1 y 0 de la característica de riesgo y rendimiento para ver qué tan bien funcionó la estrategia original.
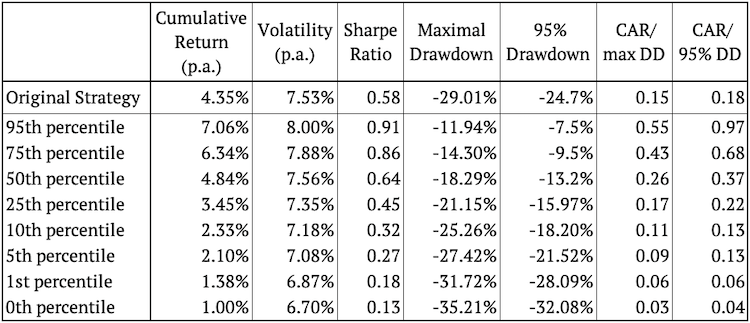
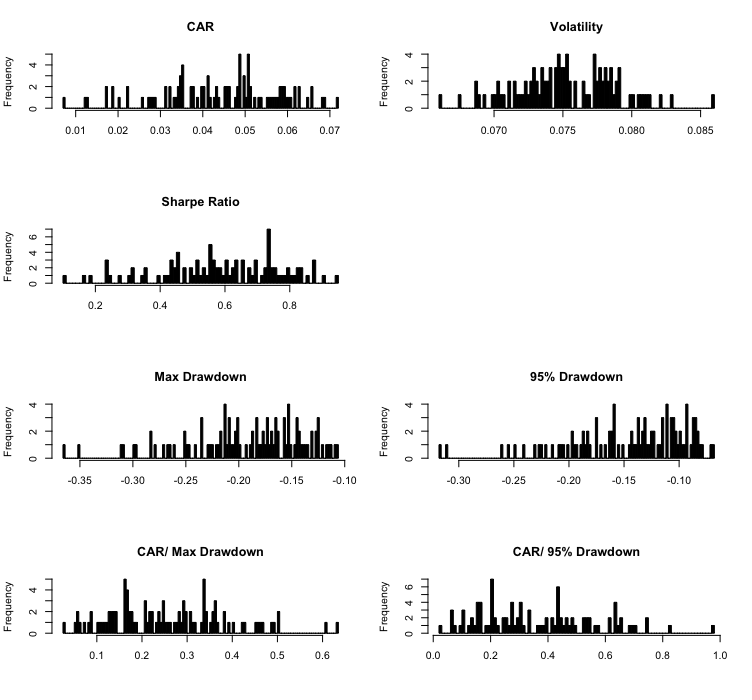
Al observar el rendimiento acumulado, la volatilidad y la relación de Sharpe, el rendimiento de la estrategia original se encuentra entre el percentil 25 y el 50. Esto indica que más de la mitad de las alteraciones aleatorias de la estrategia son finalmente mejores que la estrategia original. Cuando observamos el drawdown máximo o el drawdown del 95 %, una vez más son mejores que la estrategia original en más del 95 % de los escenarios. Esto definitivamente es alentador para la estrategia original. Además, presentamos un conjunto de histogramas que muestran la frecuencia de las características individuales de riesgo y rendimiento.
Alteraciones de retorno de Monte Carlo
Este método de Monte Carlo cambia los rendimientos elegidos al azar en una dirección aleatoria en una cantidad preestablecida. La suposición principal detrás de este método es que los rendimientos pueden simplemente volverse más pequeños o más grandes en el futuro. Es útil observar la sensibilidad de la estrategia a tal escenario.
Técnicamente, cambiamos X% de los datos por Y% . Entonces, en el primer paso, elegimos aleatoriamente el X% de los rendimientos, y luego agregamos al azar Y% o restamos Y% del rendimiento mensual elegido en el segundo paso.
Por ejemplo, si las rentabilidades mensuales fueran (0,5%, 1%, -2,5%, -3%, 0,5%, 1,5%), X = 0,5 (50%) e Y = 0,02 (2%). Una de las simulaciones podría ser (2,5%, -1%, -2,5%, -5%, 0,5%, 1,5%). El proceso se repite 100 veces con los mismos X e Y para todas las simulaciones y se calculan los rendimientos acumulativos.
Usamos X = 0.5 (50%) e Y = 0.02 (2%) en todas nuestras simulaciones. Para mayor claridad, la siguiente figura muestra solo 50 de las 100 simulaciones.
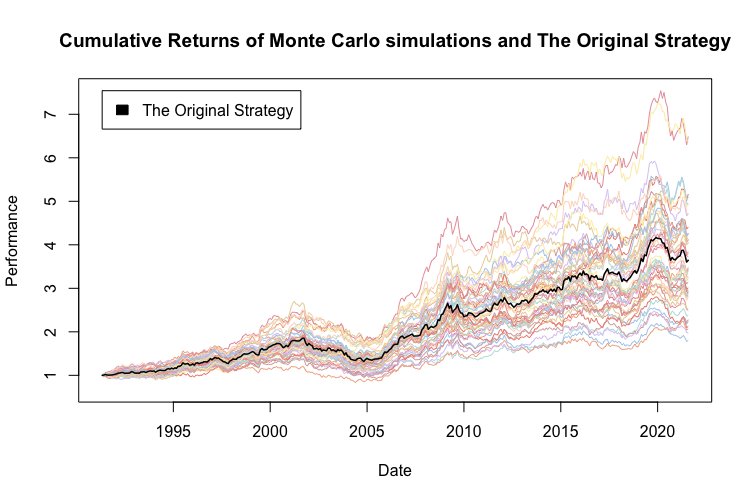
Lógicamente, al cambiar la mitad de los rendimientos, solo aumentamos la volatilidad de las simulaciones la mayor parte del tiempo. Esto también se puede observar en los resultados empíricos. Lo mismo se aplica al drawdown. Por otro lado, los retornos oscilan alrededor de la estrategia original, como se esperaba.
Una vez más, el rendimiento de la estrategia original está en el medio de las estrategias simuladas, esta vez exactamente como se esperaba. A continuación, calculamos varios percentiles de la característica de riesgo y rendimiento para ver qué tan bien se desempeñó la estrategia original en comparación con las simulaciones de Monte Carlo.
Por último, presentamos un conjunto de histogramas que muestran la frecuencia de los valores individuales de las características de riesgo y retorno.

Simulaciones de Monte Carlo de las operaciones
En la segunda sección, aplicamos los 3 métodos analizados anteriormente, sin embargo, no a simples rendimientos mensuales como los anteriores, sino a los resultados de las operaciones individuales de nuestra estrategia. Por «una operación» entendemos el retorno de una posición larga o corta para cada producto individual. Es interesante observar las diferencias entre observar únicamente los rendimientos mensuales agrupados de la estrategia y observar los rendimientos de operaciones individuales.
Muestreo de Monte Carlo sin reemplazo
Analizamos los mismos tres enfoques para las simulaciones de Monte Carlo. El primero es un muestreo aleatorio simple de transacciones sin reemplazo. Para mayor claridad, la siguiente figura muestra solo 50 de las 100 simulaciones:
Al muestrear los rendimientos de las operaciones sin reemplazo, la volatilidad de las estrategias simuladas puede o no ser la misma que la de la estrategia original. Esto depende de la construcción de la estrategia. En nuestro caso varía ligeramente. Lo mismo se aplica a los rendimientos generados por estas simulaciones comerciales de Monte Carlo. Drawdown es lógicamente completamente diferente por definición.
La siguiente tabla muestra los percentiles de las características de riesgo y retorno de las simulaciones y las características de riesgo y retorno de la estrategia original.
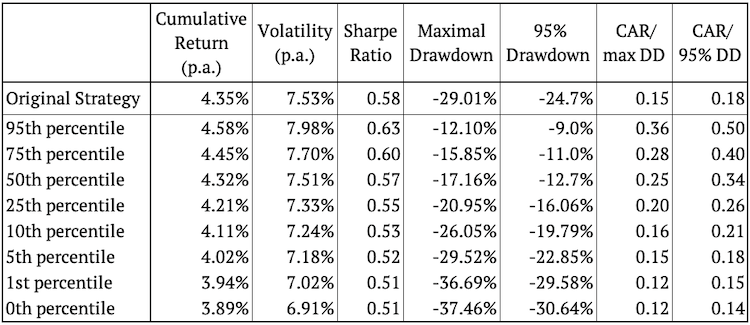
Podemos observar el mismo fenómeno que con los rendimientos mensuales: en la mayoría de las simulaciones, la cifra de drawdown es mejor que para la estrategia original. Además, también trazamos los histogramas con las frecuencias de los valores de las características de riesgo y retorno.

Muestreo de Monte Carlo con reemplazo
En segundo lugar, muestreamos 100 matrices nuevas aplicando muestreo con reemplazo a las operaciones. Se calculan los rendimientos mensuales de cada una de las 100 nuevas estrategias y se grafican los rendimientos acumulados. Para mayor claridad, la siguiente figura muestra solo 50 de las 100 simulaciones:
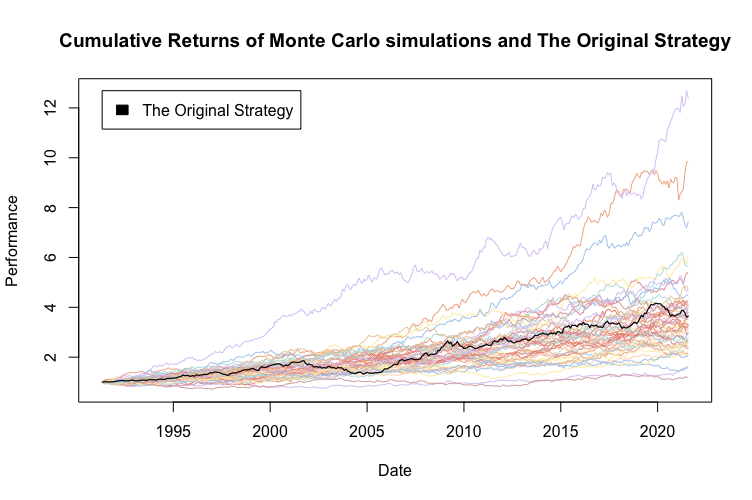
El muestreo con reemplazo siempre produce una mayor dispersión en los resultados en comparación con el muestreo Monte Carlo sin reemplazo. Este es también el caso de las rentabilidades en la simulación. Podemos observar que la volatilidad de las simulaciones de Monte Carlo es notablemente mayor y existen múltiples valores atípicos en los rendimientos simulados.
La tabla muestra que la cifra de drawdown máximo aún tiende a ser mejor para la mayoría de las simulaciones.

Alteraciones de retorno de Monte Carlo
El tercer enfoque cambia el X% de las transacciones por Y% . El proceso se repite 100 veces con las mismas X (50%) e Y (2%) para todas las simulaciones y se calculan los rendimientos de las estrategias simuladas. Para mayor claridad, la siguiente figura nuevamente muestra solo 50 de las 100 simulaciones:
En nuestro caso, la alteración del rendimiento de Monte Carlo no da como resultado una gran variación de las curvas de equidad simuladas. La razón es la construcción de nuestra estrategia (operaciones de igual ponderación) que en su mayoría promedia nuestras alteraciones de retorno aleatorias.
Esta vez, la conclusión de este análisis es bastante neutral. La mediana de las simulaciones de Monte Carlo oscila aproximadamente en torno a la estrategia original en todas las métricas de rendimiento. Además, podemos analizar los siguientes histogramas que muestran las frecuencias de valores de riesgo individual y características de retorno.

Comparación con estrategias aleatorias
Este método de Monte Carlo se utiliza para crear un conjunto de estrategias aleatorias con las que comparar la estrategia original. Se basa en la suposición de que su estrategia original debería superar a la mayoría de las estrategias aleatorias .
Nuevamente utilizamos datos sobre transacciones individuales. Técnicamente, en primer lugar, elegimos al azar qué materias primas se comercializan cada mes. En segundo lugar, apostamos aleatoriamente en posiciones largas, cortas o en efectivo con cada materia prima elegida. El proceso se repite de nuevo 100 veces. Para mayor claridad, la siguiente figura muestra solo 50 de las 100 simulaciones:
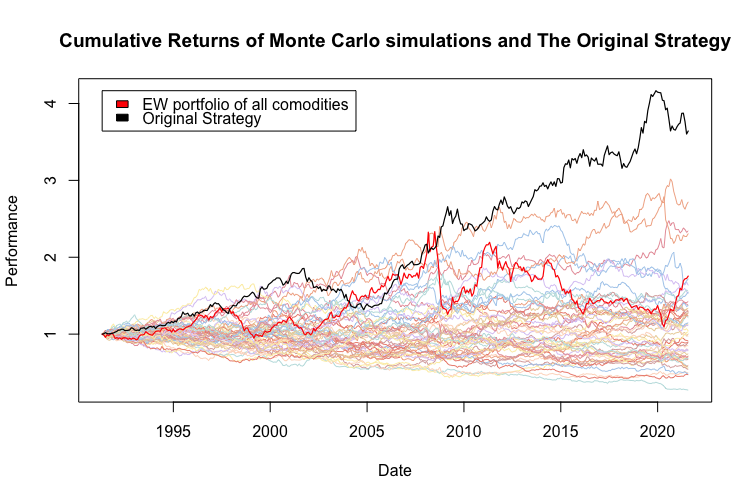
Las transacciones aleatorias, por definición, oscilan alrededor de cero la mayor parte del tiempo. Este debería ser uno de los obstáculos más fáciles de superar para su estrategia. Este conjunto de pruebas de Monte Carlo sirve como un punto de referencia independiente (de su estrategia) que debe ser superado.

Comparación de diferentes métodos Monte Carlo
Analizamos y presentamos los resultados de 4 métodos diferentes de simulación de Monte Carlo aplicados a una estrategia de trading de futuros de materias primas. Los aplicamos a ambos: rendimientos mensuales de la estrategia y operaciones individuales individuales de la estrategia.
Rentabilidades mensuales frente a operaciones individuales
La elección de utilizar rendimientos de series temporales (por ejemplo, mensuales) o rendimientos de operaciones depende en gran medida de sus necesidades. Si usted es un swing trader que se enfoca en cada operación por separado, entonces probablemente los análisis serían más adecuados para usted. Por otro lado, si usted es un inversor diversificado que promedia diferentes activos o diferentes enfoques, entonces los rendimientos de series de tiempo (rendimientos de períodos) deberían ser más fáciles de usar.
Simulaciones de estrategia de Monte Carlo sin reemplazo
Una de las simulaciones de Monte Carlo más suaves para estrategias de trading es el muestreo sin reemplazo. Este método solo cambia el orden de las rentabilidades. Por lo tanto, no cambia la volatilidad, ni el rendimiento promedio. Es principalmente útil para el análisis del drawdown y para el examen de las formas de las curvas de equidad de las estrategias. Es test de estrés para aquellos que esperan rendimientos similares para la estrategia en el futuro, simplemente ocurriendo en diferentes momentos.
Simulaciones de estrategia de Monte Carlo con reemplazo
El muestreo de Monte Carlo con reemplazo es probablemente el método más utilizado para simular escenarios hipotéticos de estrategias cuantitativas. Mediante el uso de simulaciones con reemplazo, creamos varias «nuevas historias» y aleatorizamos también el retorno y el riesgo de la estrategia. Lo utilizan aquellos que creen que los rendimientos de la estrategia se distribuirán de manera similar en el futuro, pero que no creen que serán iguales.
Alteración de retorno de Monte Carlo
La alteración de Monte Carlo de los rendimientos de la estrategia es básicamente un análisis de sensibilidad y debe usarse y percibirse como tal. Ayuda a analizar qué tan grande es el impacto de los cambios aleatorios preespecificados en una parte preespecificada de los rendimientos de la estrategia. Cuanto menos deteriorados estén los resultados de la simulación, mejor.
Comparación con estrategias aleatorias
Probablemente todo el mundo conoce al mono de Malkiel ganando a los mercados bursátiles. Siempre es útil echar un vistazo al rendimiento de su estrategia frente a estrategias aleatorias. Y este es exactamente el propósito de este método Monte Carlo. Lógicamente, uno esperaría que su estrategia supere a las variantes aleatorias de manera clara.
Conclusión
Presentamos, explicamos y analizamos múltiples enfoques para las simulaciones de Monte Carlo. También realizamos un estudio de caso real de simulaciones de Monte Carlo aplicadas a una estrategia de negociación de futuros de materias primas.
Diferentes métodos de Monte Carlo pueden ser valiosos para diferentes usuarios finales. Es crucial entender cómo funcionan y cómo interpretarlos.
Autora:
Daniela Hanicova, analista cuántica, Quantpedia
