
- Nadie cuestiona que las simulaciones de Montecarlo son una excelente herramienta para determinar los riesgos y expectativas de beneficio de cualquier producto financiero que disponga de series históricas. Sin embargo, no todos los métodos de simulación son adecuados para cualquier producto ni ofrecen respuesta a las mismas cuestiones clave.
- Artículo publicado en Hispatrading 38.
En el presente artículo analizaremos el alcance y limitaciones de tres principales enfoques a la hora de realizar este tipo de simulaciones:
- Aleatorizar la secuencia de operaciones.
- Añadir ruido a las reglas del modelo.
- Añadir ruido a las cotizaciones históricas.
Dicho de manera sencilla y sin adentrarnos en formulaciones matemáticas, una simulación de Montecarlo aplicada al trading no es más que un método de cómputo intensivo basado en generar un conjunto de datos alternativos que permiten estudiar las propiedades estadísticas de un sistema, modelo o proceso.
MÉTODO I: ALEATORIZAR LA SECUENCIA DE OPERACIONES
En Estadística se denomina muestreo de Montecarlo al procedimiento para obtener un conjunto de muestras aleatorias tomando como base una función de distribución dada. De este modo, los simuladores más simples permiten trazar los recorridos alternativos de una serie de operaciones partiendo de sus estadísticas básicas.
Por ejemplo, dado el sistema A con:
| Avg. Loss $ | Avg. Win $ | Stdev. Loss | Stdev. Win | Initial Cap. | % Win |
| -325.41 | 208.02 | 322.70 | 152.70 | 6,000 | 70.6% |
Resultados
Podemos simular los recorridos de n curvas aleatorias a partir de algún modelo de distribución. De este modo obtenemos el cono de rendimientos máximos y mínimos teóricos para un número dado de operaciones o intervalos temporales. El resultado sería similar al de la imagen inferior, siendo la curva roja superpuesta la serie original de la que proceden las estadísticas.
Sin embargo, aunque este procedimiento permite obtener resultados notablemente precisos si se utiliza bien, la mayoría de los algoritmos implementados en plataformas de trading realizan las simulaciones permutando una o varias secuencias históricas de operaciones que se toman como modelo.
Diversas aplicaciones utilizan el método del muestreo aleatorio con reposición (PCR), lo que implica que cada operación puede aparecer más de una vez en cada serie sintética generada. Esto da lugar a un gráfico en el que todas las curvas salen del mismo punto (capital inicial) y terminan en puntos distintos (beneficio acumulado):
Otras aplicaciones emplean el método de las permutaciones sin repetición (PSR), en el que cada operación de la serie original solo se emplea una vez en cada serie sintética. Las curvas de este tipo tienen un punto de origen y un punto de llegada común y realizan entre ambos un recorrido aleatorio que depende únicamente del orden que ocupa cada operación en las series generadas. Su gráfico característico es:
Ambos métodos permiten inferir numerosas propiedades del sistema o portfolio analizados, como el mayor drawdown, el capital necesario para operarlo y otras muchas propiedades estadísticas. Siendo su principal diferencia que el muestreo con reposición posibilita además hacer proyecciones sobre expectativas de beneficio en diferentes períodos determinados por la longitud de las series sintéticas a simular. Sin embargo, el muestreo sin reposición, aunque no permite realizar proyecciones debido a que el tamaño de las series es el mismo que la original, se considera más preciso para el cálculo de riesgos ya que cada serie sintética conserva las propiedades que la distribución histórica de operaciones.
Estos son los dos métodos más empleados por el software de simulación implementado en numerosas plataformas de trading y análisis financiero.
Adicionalmente, algunas aplicaciones, como AmiBroker, incorporan el método de añadir ruido a la secuencia de operaciones. Este método genera, operación por operación, pequeños cambios aleatorios para construir el conjunto de las n series sintéticas. Se trata de un abordamiento bastante controvertido ya que pequeños cambios apenas generan diversidad (aunque su efecto acumulativo en series largas puede ser grande) y los cambios de mayor amplitud pueden alterar drásticamente las propiedades de la serie original, por lo que acabaríamos con una simulación que poco tiene que ver con el modelo histórico. Independientemente de esto, la amplitud de los cambios no deja de ser otro hiperparámetro del modelo.
Los modelos de Montecarlo basados en la secuencia de operaciones no están exentos de críticas. Emilio Tomasini y Urban Jaecke en su obra Trading Systems (2009) -sumamente recomendable pese al tiempo transcurrido para todos los que se inician en esta modalidad inversora- ya nos ponen en guardia sobre algunas limitaciones evidentes de estos modelos. La principal es que la validez de la simulación depende de la calidad de los datos históricos empleados. Si los datos proceden de estrategias sobreoptimizadas, poco o nada nos dirá el método de Montecarlo sobe los riesgos ocultos de una estrategia. Tampoco tiene cada que hacer el método de Montecarlo con los cambios de marcoépoca. La mayoría de las estrategias se rompen porque sus reglas son incapaces de responder a cambios en la dinámica de los mercados que no estaban contemplados en las fases de diseño y entrenamiento. Estos cambios pueden ser bruscos o progresivos, cíclicos o completamente nuevos. En la medida en que la simulación se construye sobre una secuencia específica de operaciones, el hecho de permutar miles de veces dicha secuencia no sirve para construir escenarios alternativos que contemplen dichos cambios.
Abundando más en el tema, Michael Harris en su artículo: “Fooled By Monte Carlo Simulation” (Mayo-2017), menciona ocho situaciones en las que las simulaciones de Montecarlo basadas en aleatorizar una secuencia de operaciones pueden producir resultados erróneos:
1.- Cuando la estrategia está sobreoptimizada y/o el porcentaje de aciertos es demasiado alto.
2.- Simetría forzada o sistemas basados en la reversión de posiciones largas-cortas.
3.- Sistemas tipo Long-Term de baja cadencia.
4.- Dependencia positiva-negativa entre operaciones.
5.- Cuando la operativa toma como input la curva del equity del propio sistema.
6.- Cuando la estrategia implementa algoritmos de position sizing.
7.- Series de operaciones demasiado largas.
8.- Estrategias desarrolladas por data-mining.
Ciertamente, todos estos factores empeoran o invalidan los resultados de una simulación, siendo los más común trabajar con series sobreoptimizadas y no haber tenido en cuenta la dependencia entre operaciones. Puede tratarse de una dependencia unidimensional o bidimensional, aunque normalmente en el trading estas dependencias se deben a la proximidad temporal entre operaciones. Si no estamos completamente convencidos de la independencia entre operaciones (como de hecho ocurre en la mayoría de estrategias), podemos aplicar algún test de contraste para detectar las dependencias; por ejemplo test basados en las rachas o el test de Ljung-Box.
Las series demasiado largas, en mi opinión, no suponen mayor problema siempre y cuando el análisis se haga en dos etapas: En la primera realizamos una simulación rápida (con 500 muestras y un IC = 95% será más que suficiente) para determinar el DD máximo en una primera aproximación y calcular a partir de él el capital necesario para operar las estrategia. Hecho esto, realizamos una segunda simulación con el nivel de precisión requerido.
Las demás situaciones mencionadas por Harris son evidentes y no nos detendremos en ellas. Sin embargo, me llama mucho la atención que este autor no haya puesto el dedo en la llaga sobre los dos verdaderos problemas de las simulaciones basadas en randomizar una única secuencia de operaciones:
1.- Son simulaciones “mono-hilo”.– Una serie de datos históricos describe un único escenario, un recorrido posible de entre las múltiples configuraciones que puede adoptar el binomio sistema-mercado. Al reordenar aleatoriamente las operaciones lo único que obtenemos son variantes de ese escenario único: Las medias y las desviaciones serán las mismas, y los puntos de salida y llegada también. Otros elementos importantes en el análisis de una estrategia, como los tamaños de la peor y mejor operación o el porcentaje de aciertos, tampoco sufrirán modificación alguna.
2.- Se destruyen las marcas temporales.– Muchas veces las operaciones ganadoras y perdedoras se acomodan a una pauta temporal. Por ejemplo, años de escasa volatilidad con rendimiento nulo o negativo son seguidos por años más volátiles y con fuerte sesgo tendencial en los que se obtienen beneficios extraordinarios. No digamos si además la estrategia saca partido de determinados procesos estacionales. Toda esta información se pierde inevitablemente al randomizar la secuencia de operaciones.
MÉTODO II: AÑADIR RUIDO A LAS REGLAS DEL MODELO
Hay dos formas de hacerlo; modificando las reglas mismas o modificando los valores paramétricos. Por ejemplo, si una regla es:
SMA(200)[0] > Close[0]
Podemos introducir modificaciones cambiando el tipo de media (EMA, DEMA, TEMA, HMA, KAMA, etc.) o el punto de la barra a rebasar (Open, High, Median, Typical) y también alterando ligeramente sus valores de referencia (180, 190, 210, 220) o la barra en la que se verifica la condición (0, 1, 2). Si se trata de filtros, como por ejemplo de volatilidad, tendencia, momento o volumen) se puede introducir ruido eligiendo indicadores distintos pertenecientes a la misma familia. En algunas plataformas de Machine Learning esto puede hacerse con suma facilidad eligiendo un rango de indicadores, operadores y tipos de órdenes consecuentes con una lógica de base. Aunque aquí la dificultad radica en determinar si estas modificaciones son menores o estamos alterando la propia lógica.
Una manera más sencilla de añadir ruido a las reglas del sistema es modificando los valores paramétricos en un rango específico. El procedimiento idóneo para esto es el que yo denomino RPR (Robust Parameter Randomiztion), variante del SPR de Dave Walton; “Know Your System! – Turning Data Mining from Bias to Benefit through System Parameter Permutation” (NAAIM, Feb. 2014) que consiste en extraer muestras “n” aleatorias del conjunto “m” de combinaciones paramétricas del sistema. Dichas combinaciones están acotadas a las horquillas de valores máximos y mínimos de cada parámetro que se determinan durante el proceso de construcción.
Los elementos clave del modelo RPR son:
1.- Preparación del modelo de simulación: Estático o dinámico, tamaño del histórico, time frame, número de activos, hiperparámetros del modelo.
2.- Determinación del espacio de búsqueda: Definir el universo de combinaciones posibles y elegir un número de muestras aleatorias para un nivel de precisión dado.
3.- Ratios diana o función objetivo: Criterios empleados para ordenar en un ranking las curvas de beneficios y resultados procedentes de cada combinación paramétrica.
4.- Filtros de aceptación y rechazo: Permiten descartar automáticamente las combinaciones paramétricas improductivas: No hay operaciones, demasiadas operaciones ambiguas (por ej. entrar y salir en la misma barra), períodos demasiado largos sin operar, posiciones huérfanas (que no se cierran nunca o están demasiado tiempo en el mercado), demasiadas posiciones abiertas, etc.
5.- Análisis de resultados: Distribución del Net Profit, DDm y BMO. R/R globales y por períodos. Estudio de las curvas del beneficio y sus métricas específicas agrupadas por percentiles.
6.- Análisis dinámico (Si procede): Requiere dividir el histórico en varios subperíodos y realizar simulaciones múltiples. Es bueno para estudiar la sensibilidad de las métricas R/R en distintas configuraciones de los mercados o marcoépocas y su evolución en el tiempo. Este tipo de análisis también permite hacer ajustes periódicos en las horquillas paramétricas en caso de que algunos valores óptimos se sitúen en los extremos de los rangos establecidos.
7.- Criterios de ruptura: Determinación de los criterios de ruptura del sistema basada en los resultados del análisis multi-hilo. Normalmente los criterios se basan en la superación del DD de Montecarlo, reducción de la esperanza matemática o BMO y discrepancias en la distribución de operaciones observada y la teórica, empleando alguna prueba de contraste de hipótesis como el estadístico X2 de Pearson.
Pongamos un ejemplo:
Tomemos un sencillo sistema intradiario que opera a favor de la tendencia y tiene los siguientes parámetros, valores de salto y horquillas de máximos y mínimos determinados en la fase de diseño:
| Parámetros | Valor Máx. | Valor Min. | Intervalo | Total Valores |
| EMA L | 160 | 80 | 5 | 17 |
| EMA C | 800 | 300 | 50 | 11 |
| BB Period | 120 | 50 | 5 | 15 |
| BB StdDev | 0,8 | 0,1 | 0,1 | 8 |
| Filter Period | 16 | 5 | 1 | 12 |
| Filter Level | 30 | 15 | 1 | 16 |
| MMStop% | 1,5 | 0,5 | 0,1 | 11 |
| Total Combinaciones | 47.393.280 |
Ejemplo de sistema intradiario
Como vemos, el número de combinaciones posibles es enorme y hace inviable un procedimiento exhaustivo de optimización. Por tanto, iniciamos un proceso de Montecarlo consistente en extraer n muestras aleatorias representativas del conjunto de la población.
Supongamos que tomamos como referencia del modelo la esperanza matemática o BMO y queremos un nivel de precisión de $0,5 para un nivel de confianza del 95% (z=1,96).
El primer paso será realizar una simulación a pequeña escala que no nos lleve demasiado tiempo (por ej. 300-500 iteraciones) para aproximar la desviación de resultados:
Obtenemos μ =$41,97 y σ = $8,05
Resolvemos la ecuación:
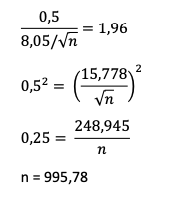
Así que redondeamos la simulación a 1.000 iteraciones.
Para implementar el proceso aleatorio en una plataforma de trading tenemos dos opciones:
- Introducir variables aleatorias en las reglas. Por ejemplo crenado en C# series aleatorias:
private Random rand = new Random();
Para luego introducirlas en los parámetros como:
rand.Next(x,y). Donde x, y son los valores máximos y mínimos.
- Si queremos evitar el inconveniente de hacer numerosas modificaciones en el código, podemos utilizar el optimizador genético poniendo el valor 1 para el número de generaciones y 1.000 para el tamaño de la población. Por ejemplo, en NinjaTrader:
De este modo, el algoritmo genético creará una población aleatoria de 1.000 elementos y el optimizador irá generando secuencialmente los resultados de cada combinación paramétrica. Luego no tenemos más que exportarlos a Excel para realizar nuestro análisis.
En las imágenes inferiores mostramos los gráficos de distribución del BMO, Net Profit y DDm:
Como podemos ver el DD de Montecarlo oscila entre un máximo de -$20.884, al que no prestamos atención por tratarse de una configuración paramétrica de caso único y unos valores CDaR (Conditional Drawdown at Risk) de -$13.146 y -$14.960 para unos niveles de confianza del 95% y 99% respectivamente.
En la distribución del BMO el valor relevante es la mediana ($41,4) que nos servirá para determinar configuraciones de la estrategia sobreoptimizadas (por encima) e infraoptimizadas (por debajo). También interesa saber si en el marco histórico analizado existen combinaciones paramétricas con esperanza matemática negativa y cuántas. En este caso vemos que el valor mínimo de la simulación es de $13,20. Por tanto, no hay curvas con rendimiento negativo en esta simulación, si bien veremos una enorme dispersión de resultados.
Nuestro siguiente paso es construir la tabla de percentiles para BMO y DDm:
| Percentil | BMO | DDm | Zonas |
| 1 | 76,06 | -3.184 | ACEPTACIÓN |
| 0,99 | 64,59 | -4.092 | |
| 0,95 | 58,54 | -4.838 | |
| 0,9 | 54,20 | -5.343 | |
| 0,85 | 51,88 | -5.800 | |
| 0,8 | 49,98 | -6.085 | |
| 0,75 | 48,12 | -6.382 | |
| 0,7 | 46,45 | -6.669 | |
| 0,65 | 44,81 | -6.974 | |
| 0,6 | 43,58 | -7.276 | |
| 0,55 | 42,53 | -7.600 | |
| 0,5 | 41,40 | -7.873 | |
| 0,45 | 40,17 | -8.142 | |
| 0,4 | 38,99 | -8.449 | |
| 0,35 | 37,73 | -8.784 | |
| 0,3 | 36,33 | -9.098 | |
| 0,25 | 34,85 | -9.576 | ALARMA |
| 0,2 | 33,47 | -10.242 | |
| 0,15 | 31,33 | -10.902 | |
| 0,1 | 28,83 | -11.954 | |
| 0,05 | 25,65 | -13.147 | |
| 0,01 | 18,46 | -14.960 | RECHAZO |
| 0 | 13,20 | -20.885 |
Los percentiles más altos de la tabla > 85% corresponden a un rendimiento extraordinario que pocas veces veremos en operativa real, mientras que el régimen normal de funcionamiento se sitúa en una ancha banda por encima (50%-80%) y por debajo (30%-50%) de la mediana. Los percentiles (5%-25%) evidencian un comportamiento pobre, que de no superarse en el tiempo, nos situarían en la zona de alarma. El rebasamiento de percentiles inferiores tiene dos lecturas:
- Estancamiento: Cuando el BMO se sitúa en los niveles más bajos por largos periodos pero el DDm. pero el DDm no alcanza niveles preocupantes. Si se prolonga por periodos inusualmente largos, podemos considerar la ruptura del sistema.
- Pérdidas inasumibles: El rebasamiento del DD de Montecarlo o CDaR al 95% certificaría la ruptura de la estrategia obligándonos a detener la operativa.
El enfoque dinámico de este modelo tiene la ventaja de permitirnos rastrear en el tiempo las variaciones en la distribución del Net Profit, BMO y DDm y otros ratios clave. Con este tipo de análisis podremos estudiar tres cuestiones de capital importancia:
- Sensibilidad de la lógica del sistema a los diferentes regímenes del mercado: Alta o baja volatilidad y estructura alcista o bajista de fondo.
- Efecto “Cisne Negro”: Comportamiento del sistema en situaciones extremas de los mercados. Por ejemplo, la crisis de 2008.
- Deterioro progresivo: Desgaste acumulativo de la estrategia desde la fase de diseño en adelante.
En el siguiente gráfico podemos ver una simulación dinámica (1.000 iteraciones x período) del BMO y DDm en intervalos temporales de 2 años:
Como podemos observar ambos ratios experimentan considerables fluctuaciones en sus valores máximos y mínimos, lo que evidencia una alta sensibilidad de la estrategia a los cambios de marcoépoca. Particularmente, a las variaciones en la volatilidad media del mercado. Por lo que respecta al DDm, observamos un pico en el bienio 2016-17 lo suficientemente acusado como para ponernos en guardia ante posibles riesgos ocultos de la estrategia. Si bien el resto de los periodos son bastante estables considerando tanto la mediana como el CDaR.
Otro estudio interesante que nos permite el enfoque dinámico es la evolución de los valores paramétricos de referencia en los distintos períodos. Normalmente cuando se realiza una situación tipo Walk-Forward se entrena el sistema en distintas regiones in-sample (IS) y se aplican las mejores combinaciones paramétricas de cada período de entrenamiento a las regiones out-sample (OS), normalmente contiguas. Realmente no hay ningún motivo para elegir los mejores valores obtenidos en el IS como valores idóneos para el OS, salvo la creencia – por cierto bastante acrítica– en el Principio de Estabilidad: “Lo que mejor ha funcionado antes es lo que más probabilidades tiene de seguir funcionando en un horizonte inmediato”.
En realidad podríamos razonar a la inversa y pensar que estas combinaciones idóneas para el IS, darán lugar en el OS a una progresiva, e incluso súbita, reducción del rendimiento, debido al fenómeno de la sobreoptimización. Lo cual no habría ocurrido si se utilizan combinaciones próximas a la mediana del “análisis multi-hilo” o incluso cualquier combinación elegida al azar dentro de la zona robusta.
Precisamente para analizar la variabilidad paramétrica en el tiempo nos resultará de enorme utilidad este enfoque dinámico. En el gráfico inferior la evolución de los valores de máximo, mínimo rendimiento y próximos a la mediana de algunos parámetros clave:
Como muestran estos gráficos, los parámetros de máximo y mínimo rendimiento fluctúan enormemente entre períodos, por lo que no hay ninguna garantía de que los mejores de un intervalo temporal sean también los mejores en intervalos contiguos. Esto es así debido a la propia dinámica de los mercados en los que los cambios de régimen se suceden de manera imprevisible.
El método RPR, en su versión dinámica, permite ir más allá de una mera simulación de Montecarlo y realizar otros tipos de análisis como stress tests o pruebas de resistencia para identificar fallos en las reglas, errores en la determinación de las zonas robustas o el desgaste progresivo de la lógica con independencia de una configuración paramétrica dada.
Esto último es lo que mostramos en el siguiente gráfico:
Podemos caracterizar el desgaste de fondo como la regresión lineal de la mediana del Net Profit obtenido en cada una de las 6 simulaciones RPR. Pese a que las combinaciones paramétricas de máximo rendimiento muestran un repunte en 2018, la pendiente de la mediana es negativa lo que evidencia una progresiva pérdida de sensibilidad de la lógica de base con independencia de los parámetros.
En el próximo artículo seguiremos hablando de algunos aspectos importantes.
