![]()
Encontrar una buena fuente de datos con datos de extensa y de calidad es uno de los mayores desafíos en el trading cuantitativo. Definitivamente hay algunas fuentes de datos con muy extensas. Sin embargo, tienden a estar en el lado más caro. Por otro lado, los datos baratos o gratuitos suelen carecer de calidad y/o tienen plazos más cortos.
Este artículo explica cómo combinar varias fuentes de datos para crear un historial de datos diarios de 100 años para los bonos estadounidenses a 10 años. Tener un historial de 100 años de datos diarios puede ser muy beneficioso para comprender los patrones del mercado, analizar el historial y ampliar las pruebas retrospectivas para llegar a una nueva fuente de datos fuera de la muestra.
Además, suponga que desea examinar cómo se habría comportado su cartera durante varios eventos históricos o realizar una prueba retrospectiva de una estrategia durante múltiples fases del mercado. En ese caso, un extenso historial brinda más oportunidades. Además, los inversores siempre están a la carrera para comprender mejor el mercado. Por lo tanto, tener un conocimiento sustancial de la historia es crucial.
Datos subyacentes y fuentes de datos
Para crear historial de 100 años de bonos estadounidenses a 10 años, hemos combinado varias fuentes de datos:
1926 – 1962: rendimiento mensual de los bonos estadounidenses a 10 años
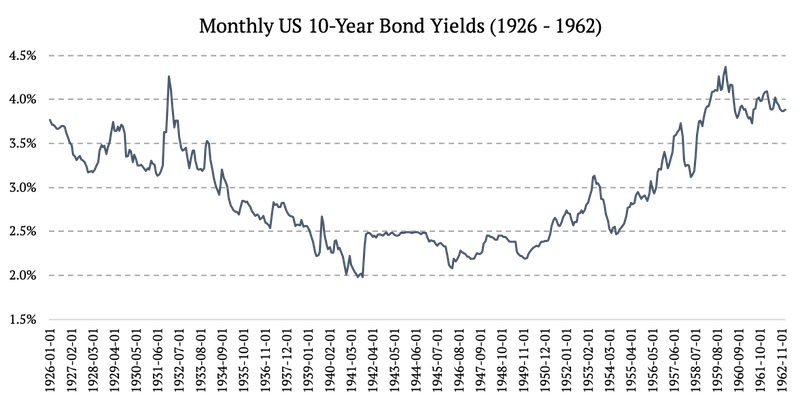
Fuente: https://fred.stlouisfed.org/series/LTGOVTBD
1962 – 2002: Rendimiento diario de los bonos estadounidenses a 10 años
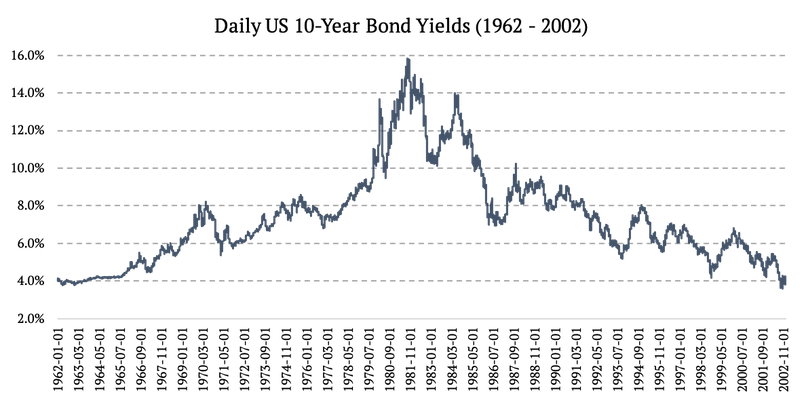
Fuente: https://fred.stlouisfed.org/series/DGS10
2002 – 2022: IEF ETF (ETF de bonos del Tesoro iShares de 7 a 10 años)
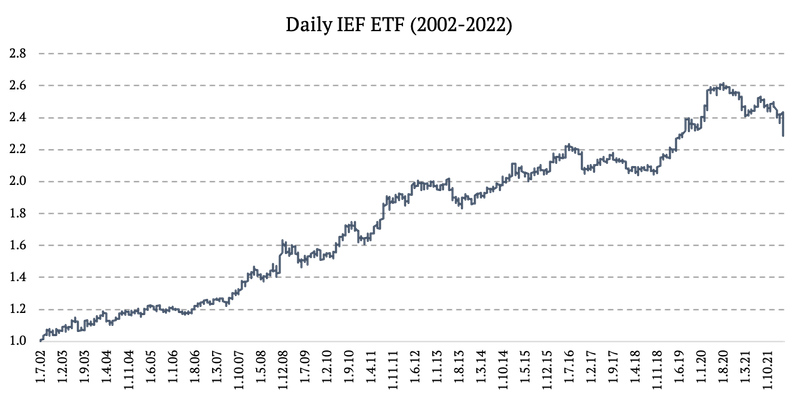
Fuente: https://finance.yahoo.com/
Cómo transformar los rendimientos de los bonos en rendimientos totales
De 1926 a 1962 se trabajó con rendimientos mensuales. Primero, necesitábamos transformar los rendimientos de los bonos en rendimientos totales. Afortunadamente, una vez que tiene una serie temporal de rendimientos, también puede saber muy bien el rendimiento total del respectivo bono. ¿Cómo? Te lo mostraremos a continuación. De manera simplificada, cada mes, un bono en particular:
- Gana una fracción de carry (rendimiento al vencimiento) equivalente a aproximadamente 1/12 del YTM
- Se revaloriza por la variación de este rendimiento:
- Si los rendimientos aumentan, el valor de un bono disminuirá en (aumento del rendimiento)*(duración)
- Si los rendimientos caen, el valor de un bono aumentará en (caída del rendimiento)*(duración)
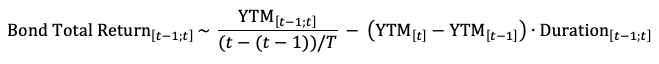
Ya tenemos una serie temporal de rendimientos de bonos. Ahora, ¿cómo obtenemos la serie de tiempo para la duración? Incluso en esto, podemos aproximarnos. Sin embargo, primero debemos entender y decidir si queremos crear una serie de tiempo de duración constante o una serie de tiempo de madurez constante.
Serie de Bonos de Duración Constante
La duración constante es lo más fácil. Simplemente asumimos que la duración de nuestro vínculo es constante. Por ejemplo, podemos suponer que la duración de un bono del Tesoro de EE. UU. a 10 años se mantendrá en 8 años.
Sin embargo, en realidad, esto a menudo no es el caso. En realidad, si tiene un bono del Tesoro estadounidense a 10 años y su rendimiento cae significativamente, su duración aumentará. Esto es causado por la llamada convexidad del enlace.
Lo mismo se aplica en la dirección inversa: si el rendimiento de un bono aumenta significativamente, su duración se reducirá. Por lo tanto, si uno quiere mantener una «serie de duración constante», necesita comprar vencimientos ligeramente más largos o más cortos de un bono en particular en función de cómo se mueven los rendimientos.
Serie de Bonos de Vencimiento Constante
La mayoría de los ETF tienen como objetivo un vencimiento específico (por ejemplo, de 7 a 10 años), los futuros de bonos también están vinculados al vencimiento y muchos índices y series de datos de rendimiento también son series temporales de vencimiento constante.
Cuando calculamos el rendimiento total del bono de vencimiento constante, asumimos que el vencimiento no cambia (en nuestro caso, 10 años durante todo el tiempo), sin embargo, la duración cambia, porque los rendimientos sí cambian (como se describió anteriormente, debido a la convexidad efecto).
Afortunadamente, no es tan difícil derivar la duración de un bono de vencimiento constante si ya tenemos a mano una serie de datos de rendimiento, lo cual, por supuesto, tenemos.
Cálculo del rendimiento total de un bono
Como se mencionó anteriormente, para calcular el rendimiento total de un mes específico, en primer lugar, tuvimos que calcular la duración. Afortunadamente, Excel tiene una función integrada, MDURATION, que calcula la duración a partir del rendimiento y la fecha respectivos (asumimos un bono de cupón cero).
Ahora que tenemos la serie temporal de rendimientos y duración del bono, calculemos el rendimiento total para un mes específico utilizando la siguiente fórmula:
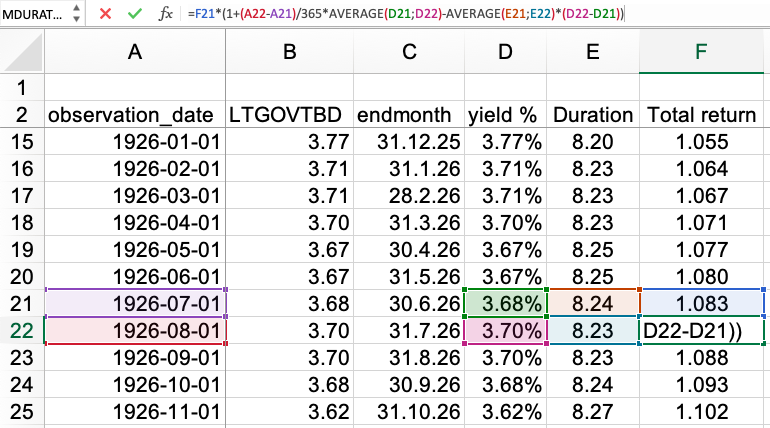
Entonces, los elementos principales en la fórmula son: el rendimiento total de ayer (F21), el número de días entre los meses individuales (A22-A21), el promedio de dos rendimientos consecutivos (D21; D22), el promedio de dos valores consecutivos de duración (E21;E22), y la diferencia entre el rendimiento de hoy y el último rendimiento (D22-D21).
1926 – 1962: rendimiento total de un bono estadounidense a 10 años calculado a partir de los rendimientos mensuales
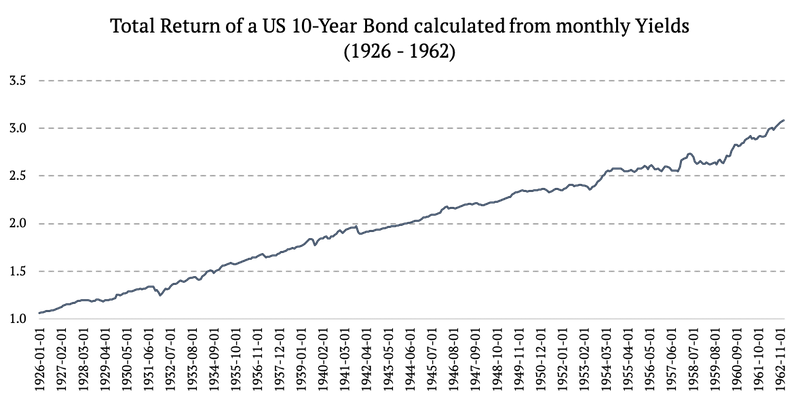
1962 – 2002: Rentabilidad total de un bono de EE. UU. a 10 años calculado a partir de los rendimientos diarios (el gráfico a continuación usa el eje y log2)
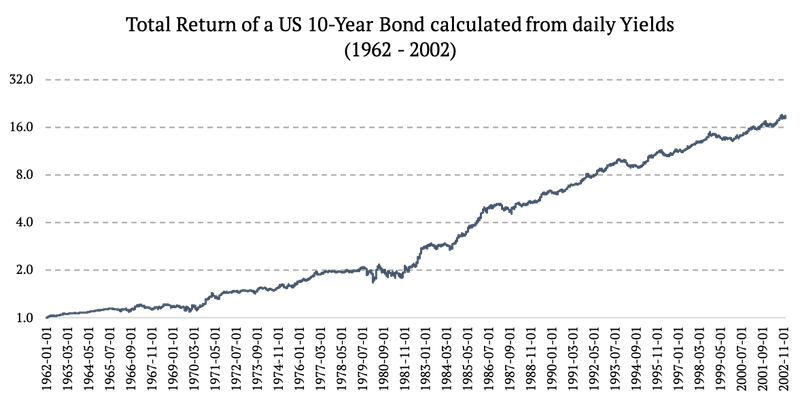
Transformación de datos mensuales en datos diarios
En las secciones anteriores, creamos una serie temporal de rendimiento total para un bono del Tesoro de EE. UU. a 10 años desde 1926. Sin embargo, la parte de los datos desde 1926 hasta 1962 tiene únicamente una frecuencia mensual. Entonces, ¿cómo llegamos a un dato diario? Tenemos que transformar los rendimientos totales mensuales en rendimientos totales diarios.
Como se mencionó anteriormente, el punto de datos histórico diario más antiguo para los rendimientos a 10 años de EE. UU. comienza en 1962. Los datos más antiguos son solo mensuales. Sin embargo, tenemos datos diarios para letras del Tesoro de 3 meses de https://fred.stlouisfed.org/series/DTB3 . Supongamos ahora que las letras del Tesoro están altamente correlacionadas con los bonos del Tesoro en un marco de tiempo intramensual (diario). O, si le damos la vuelta, ¿puede encontrar algo con datos diarios de 1954 a 1962 que esté más correlacionado con los bonos del Tesoro de EE. UU. que con las letras del Tesoro de EE. UU.? Probablemente no.
Tomado como base esta suposición, podemos extrapolar la volatilidad diaria de las letras del Tesoro de EE. UU. a 3 meses y aplicar esta volatilidad intramensual (diaria) a nuestra serie temporal mensual de rendimientos del Tesoro. Lo llamamos una «extrapolación de proxy de volatilidad», y nuestro proxy serán las letras del Tesoro de EE. UU.
Dividimos el período mensual 1926-1962 en dos subperíodos: 1926-1954 y 1954-1962. Para el primer período, aplicamos una interpolación lineal ingenua para llegar a los datos diarios. Para el segundo período aplicamos nuestra extrapolación de proxy de volatilidad, que describimos a continuación en detalle.
Interpolación linear
Desafortunadamente, no existe un proxy diario para la volatilidad de los bonos antes del año 1954. Por lo tanto, aplicamos una interpolación lineal simple en este primer subperíodo. Cada mes calculamos la diferencia acumulada entre los dos puntos de datos para obtener el interés diario. Luego acumulamos los intereses respectivos cada día. El principal inconveniente es que la curva de renta variable resultante tiene una volatilidad intramensual cero.
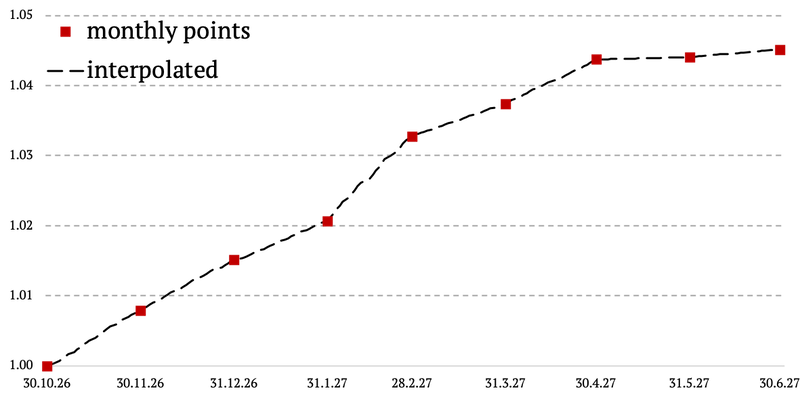
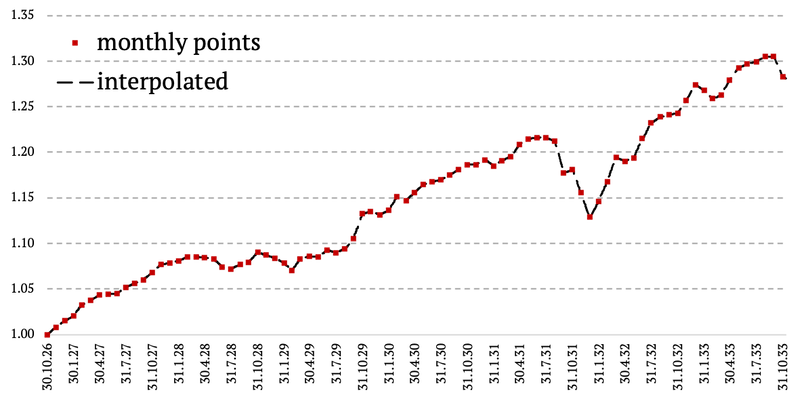
Extrapolación del proxy de volatilidad
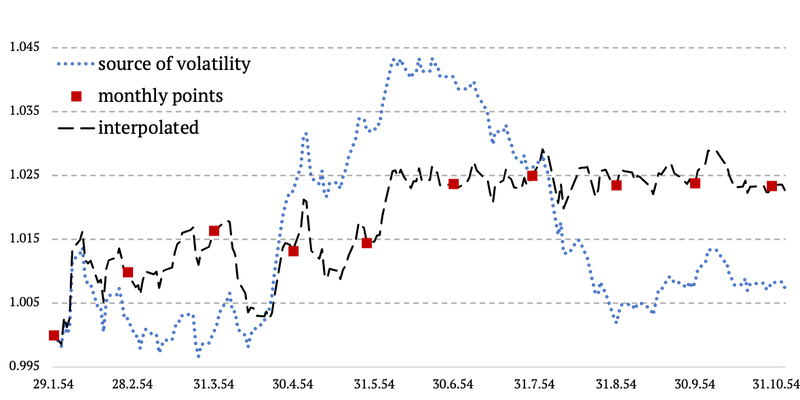
Esta vez implementamos la volatilidad desde un proxy externo: las letras del Tesoro de EE. UU. Los puntos de datos mensuales de nuestros datos originales (valores del Tesoro de EE. UU. a 10 años, rendimiento total) permanecieron intactos. Lo único que cambiamos es agregar una volatilidad intramensual (diaria) con una correlación realista con los mercados de bonos (T-bills de EE. UU.).
Cada mes, calculamos la diferencia acumulada mensual del proxy (T-bills) y la restamos de la diferencia acumulada mensual de nuestro bono estadounidense a 10 años y la dividimos por la cantidad de días de negociación en el mes respectivo. Obteniendo así la volatilidad diaria. El último paso fue calcular la rentabilidad diaria acumulada del bono estadounidense a 10 años.
Esta metodología probablemente se entienda fácilmente con un simple gráfico. Lo que básicamente hacemos es que copiamos la volatilidad diaria de las letras del Tesoro de 3 meses y las conectamos entre dos puntos de datos mensuales de los bonos del Tesoro de EE. UU. a 10 años. Y nos aseguramos de que no haya saltos ni lagunas en los datos y que todo suceda de forma lineal. Vea el gráfico a continuación.
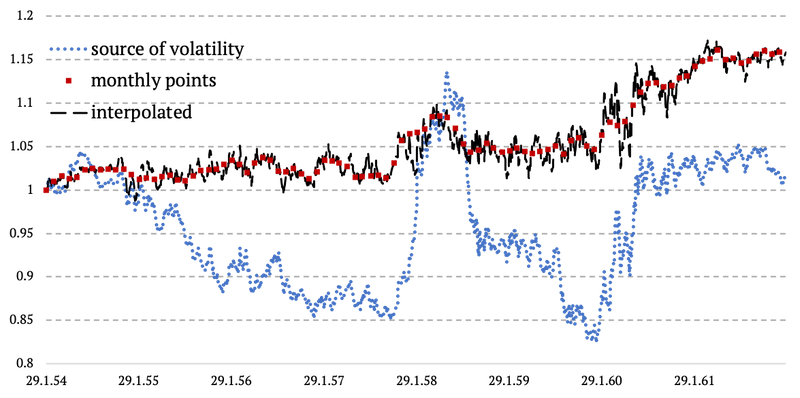
Combinación de varias fuentes de datos
Ahora que creamos con éxito series de datos diarios desde 1926 hasta 1962, debemos dar un último paso. Dicho esto, finalmente combinamos los cuatro períodos de diferentes cálculos y fuentes de datos en una serie temporal:
- 1926 – 1954: rendimiento total diario interpolado linealmente,
- 1954 – 1962: Proxy de volatilidad rendimiento total diario extrapolado,
- 1962 – 2002: rendimiento total de los rendimientos diarios de los bonos estadounidenses a 10 años,
- 2002 – 2022: IEF ETF (ETF de bonos del Tesoro iShares de 7 a 10 años).
La siguiente figura usa el eje y log2.
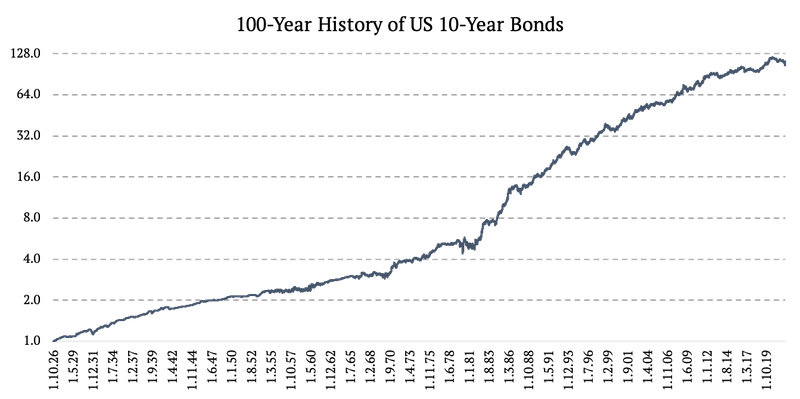

Pingback: Ampliación de los datos históricos diarios de materias primas a 100 años [Estudio] por Quantpedia
Pingback: Las peores caídas o crash de un solo día y los mayores eventos geopolíticos del siglo pasado por Quantpedia
Pingback: Cómo replicar cualquier cartera por Quantpedia