">
">
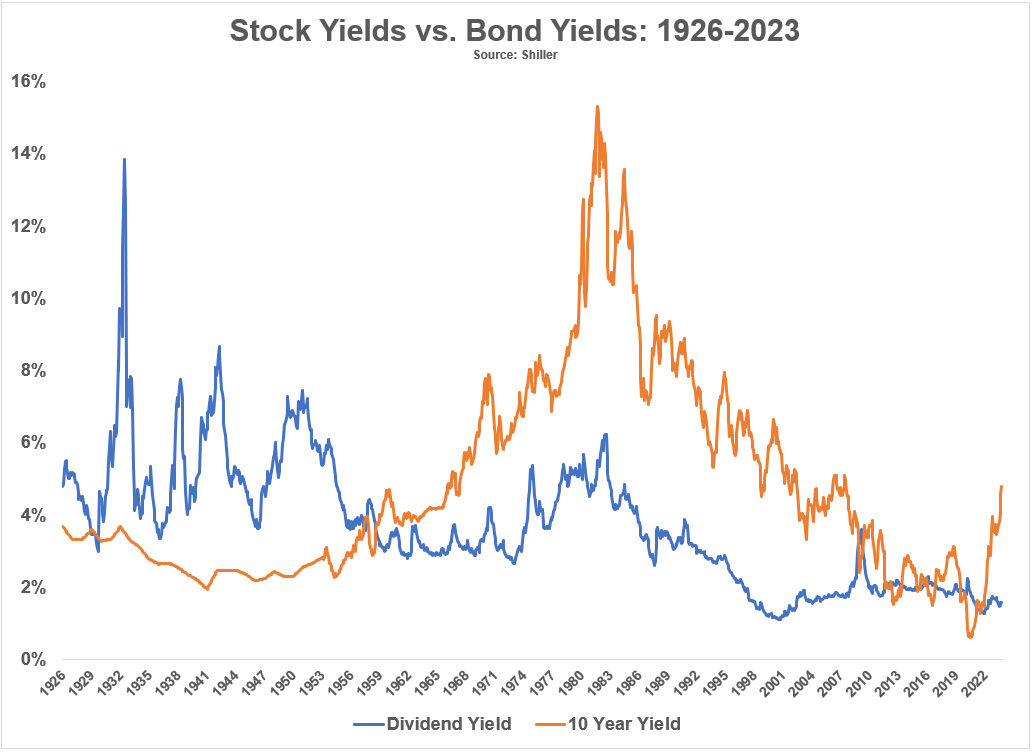
¿Qué impulsa los bonos? por Dr. Ed Yardeni

En su entrevista del jueves con David Westin de Bloomberg en el Club Económico de Nueva York, se le preguntó al presidente de la Reserva Federal, Jerome Powell, sobre el impacto bajista de la creciente oferta de deuda gubernamental en el mercado de bonos, dado que la Reserva Federal ya no compra títulos del Tesoro y que los extranjeros, según se informa, también están reduciendo sus compras. Powell respondió que las compras por parte de extranjeros “en realidad han sido bastante sólidas” este año.
Esa declaración nos brinda a Melissa y a mí la oportunidad de actualizar nuestro análisis de la oferta y la demanda en el mercado del Tesoro. Considera lo siguiente:
(1) Bajistas versus alcistas. En nuestra sesión informativa matutina del 14 de agosto, titulada “Desinversión”, escribimos: “La oferta y demanda de bonos no suele ser tan importante para la determinación del rendimiento de los bonos como lo son la inflación real y esperada y las expectativas de cómo responderá la Reserva Federal ante ellos”. El rendimiento de los bonos del Tesoro a 10 años era del 4,19% en ese momento, pero nos preocupaba cada vez más que subiera debido al desequilibrio entre la oferta y la demanda.
Observamos que favorecer a los bajistas en el mercado de bonos “es el rápido aumento del déficit federal y la evidencia de que la demanda puede no igualar la oferta de títulos del Tesoro a menos que sus rendimientos sigan aumentando. En nuestra opinión, favorecer a los alcistas es que desde el verano pasado la inflación ha mostrado una tendencia a la moderación que debería persistir hasta 2025 sin más aumentos en la tasa de los fondos federales”.
La inflación mantiene una tendencia a la moderación. Sin embargo, el rendimiento de los bonos se sitúa ahora en torno al 5,00%, ya que las preocupaciones sobre la oferta han aumentado junto con la deuda federal. La oferta se convirtió en un problema importante cuando el Tesoro anunció aumentos significativos en sus subastas el 31 de julio. De julio a septiembre, el Tesoro necesitó pedir prestado 1,01 billones de dólares, 274.000 millones de dólares más de lo anunciado en mayo. El día después de ese anuncio, el 1 de agosto, Fitch Ratings rebajó la calificación crediticia del gobierno de AAA a AA+. Eso subrayó la importancia del despilfarrador endeudamiento del gobierno y acentuó las preocupaciones de los inversores sobre la oferta.
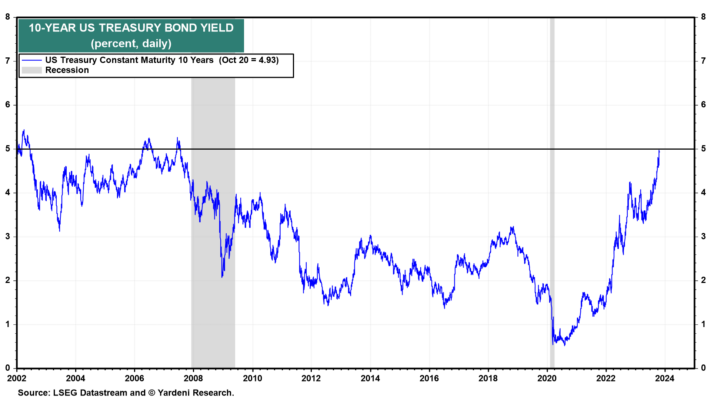
(2) ¿Es el 5% suficiente? La pregunta ahora es si el rendimiento de los bonos del Tesoro a 10 años, de 4,93% el viernes, es lo suficientemente alto como para atraer suficientes compradores de bonos para equilibrar la oferta y la demanda del mercado. Creemos que sí. El rendimiento a 10 años ha vuelto a alcanzar la lectura más alta desde junio de 2007 (Fig. 1). Anteriormente hemos caracterizado el rango de rendimiento de los bonos de 4,50%-5,00% como un retorno al antiguo rango normal antes de la Gran Crisis Financiera de 2003 a 2007. La gran diferencia entre ahora y entonces es el tamaño de los déficits federales, que es en parte al rápido aumento de los desembolsos netos por intereses del gobierno federal.
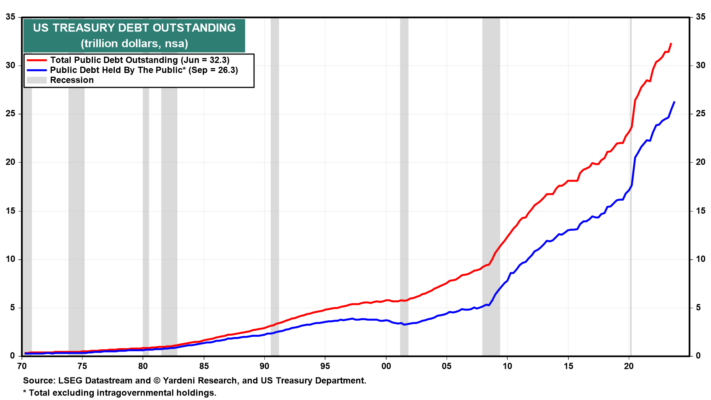
(3) Los Vigilantes de los Bonos son más fuertes que nunca. El riesgo en el mercado de bonos es que la diferencia en el factor de oferta pueda impulsar los rendimientos por encima del 5,00%. Ésa es otra forma de decir que el riesgo es que los Vigilantes de los Bonos tomen el control del mercado, elevando tanto los rendimientos que provoquen una crisis crediticia y una recesión. Ésa puede ser la única manera de obligar a Washington a reducir la trayectoria insostenible a largo plazo del déficit federal. Después de todo, Washington ha otorgado a los Vigilantes de los Bonos más poder que nunca al aumentar tan rápidamente la deuda del gobierno en los últimos años (Gráfico 2). La deuda pública total pendiente, excluyendo las tenencias intragubernamentales, se ha cuadruplicado desde el cuarto trimestre de 2008 a 26,3 billones de dólares en septiembre.
No debe olvidarse que los rendimientos elevados de los bonos pueden tener el mismo efecto de endurecimiento monetario en la economía que las elevadas tasas de los fondos federales, si no un efecto de endurecimiento mayor.
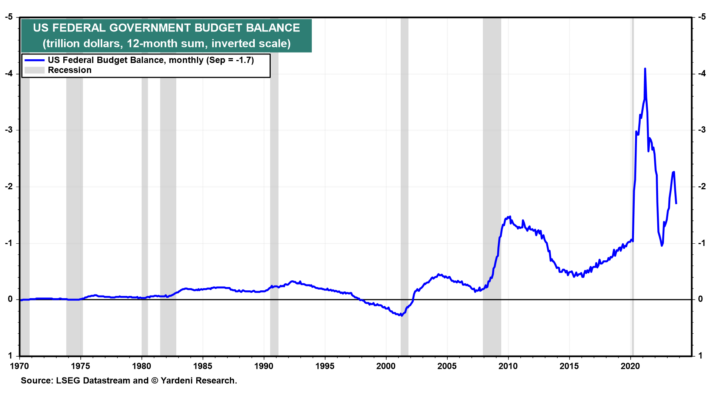
(4) La cosecha de bonos nunca falla. Durante el año fiscal 2023 (que finaliza en septiembre), el déficit federal ascendió a 1,7 billones de dólares. Esta cifra supera con creces el récord previo a la pandemia de 1,1 billones de dólares durante los 12 meses hasta febrero de 2020 (Fig. 3). Los desembolsos ascendieron a 6,1 billones de dólares, mientras que los ingresos ascendieron a 4,4 billones de dólares (Fig. 4).
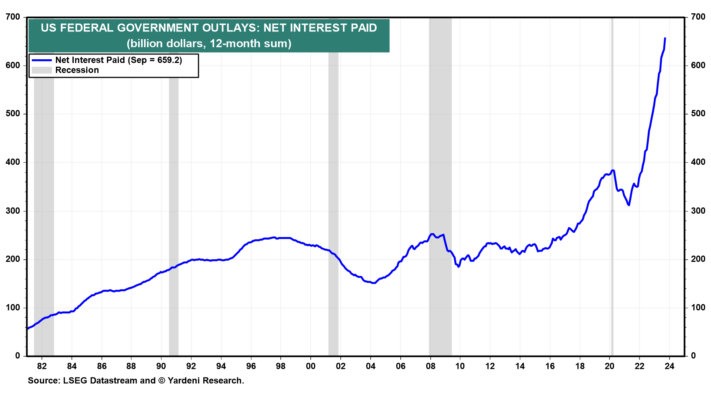
Lo que ha exacerbado el déficit federal ha sido el rápido aumento de los desembolsos en concepto de intereses netos (Fig. 5). En los últimos 12 meses hasta septiembre, ascendió a 659.000 millones de dólares, duplicándose desde mayo de 2021. La tasa de interés promedio de la deuda del gobierno es actualmente de alrededor del 2,50%. El rendimiento del Tesoro a 2 años supera actualmente el 5,00%. Por lo que este desembolso seguirá siendo el que más crecerá en los próximos meses.
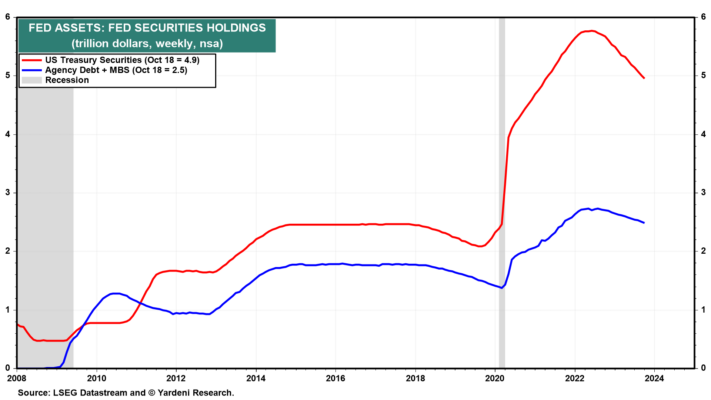
(5) La Reserva Federal y los bancos son vendedores netos. Por el lado de la demanda, la Reserva Federal dejó de comprar títulos del Tesoro durante junio de 2022 y ha dejado que sus tenencias disminuyan a medida que vencen. Durante este período de ajuste cuantitativo (QT), estas tenencias alcanzaron un máximo récord de 5,77 billones de dólares a principios de junio de 2022 y se redujeron a 4,96 billones de dólares a principios de octubre de este año (Fig. 6). Eso supone una disminución promedio de 51 mil millones de dólares al mes durante ese período de 16 meses. Si QT continúa reduciendo las tenencias de bonos del Tesoro de la Reserva Federal a aproximadamente este ritmo, otros compradores tendrán que refinanciar la disminución de 600 mil millones de dólares, en 12 meses, en las tenencias de la Reserva Federal.
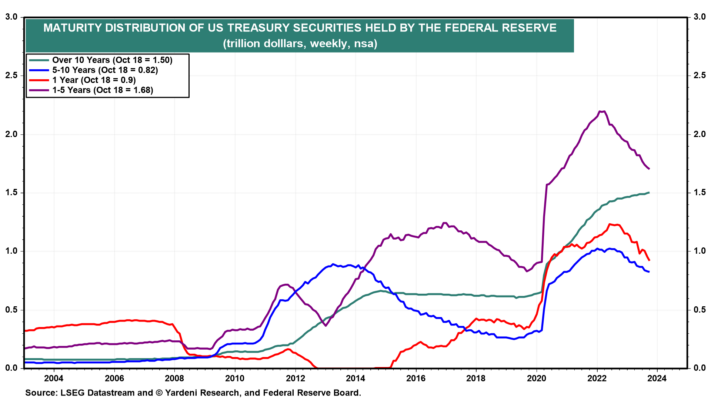
Curiosamente, las tenencias de la Reserva Federal de bonos del Tesoro con vencimiento a 10 años en realidad aumentó ligeramente durante este período en 80 mil millones de dólares (Figura 7).
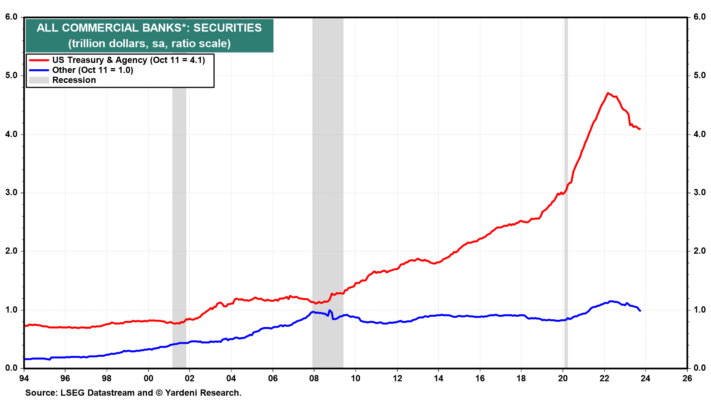
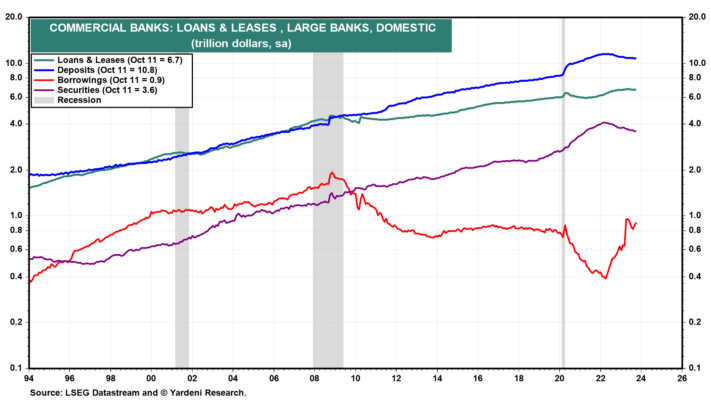
Las tenencias de valores del Tesoro y de agencias de Estados Unidos en poder de todos los bancos comerciales estadounidenses alcanzaron un máximo de 4,71 billones de dólares durante la semana del 1 de marzo de 2022 y cayeron 610 mil millones de dólares a 4,10 billones de dólares durante la semana del 11 de octubre (Fig. 8). Ese período coincide con el QT de la Reserva Federal. Esto se debe a que QT ha estado reduciendo los depósitos de los bancos, obligándolos a recaudar fondos dejando que sus títulos venzan (Fig. 9).
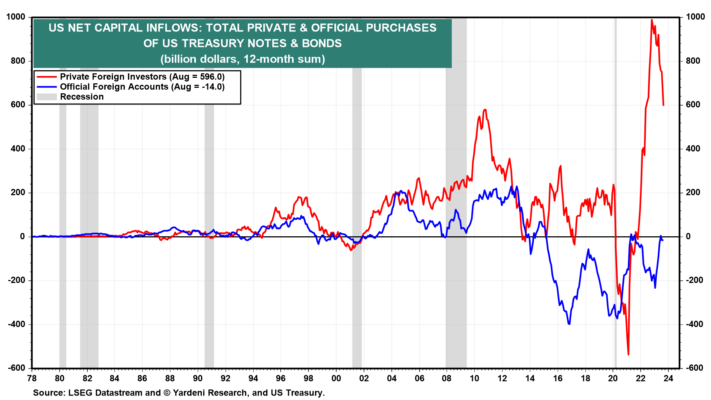
(6) Los extranjeros siguen comprando. El presidente de la Reserva Federal, Powell, tiene razón acerca de los extranjeros. Siguen siendo compradores activos de bonos estadounidenses. Según datos del Tesoro Internacional Capital (TIC), durante los 12 meses hasta agosto, sus compras netas de bonos estadounidenses fueron de 582 mil millones de dólares, incluidos 596 mil millones de dólares comprados por privados extranjeros y 14 mil millones de dólares vendidos por cuentas oficiales en el extranjero (Fig. 10). Durante los últimos tres meses hasta agosto, los inversores extranjeros compraron 75.000 millones de dólares en notas y bonos del Tesoro de Estados Unidos, los extranjeros privados compraron 79.300 millones de dólares y las cuentas oficiales privadas vendieron 4.300 millones de dólares.
(7) Los inversores nacionales individuales e institucionales son las incógnitas conocidas. En los últimos 12 meses, los fondos mutuos de bonos y los ETF han tenido entradas netas de 194.100 millones de dólares. Desafortunadamente, los inversores acudieron a estos fondos a un ritmo récord, que alcanzó un máximo de 1,0 billón de dólares durante 2021 en una suma de 12 meses, cuando las tasas de interés estaban en mínimos históricos o cerca de ellos. Es evidente que los inversores individuales e institucionales han acumulado enormes pérdidas realizadas y no realizadas en el mercado de bonos.
La pregunta es si los rendimientos de los bonos superiores al 5,00% ahora atraerán a los inversores de vuelta al mercado de bonos. Creemos que sí.


 ">
">


 ">
">

 Una amistad o una relación romántica puede superar muchos altibajos. A veces, durante nuestro dolor, puede parecer que nuestro afecto se ha desvanecido. A menudo, sin embargo, podemos volver a la cercanía porque nuestro dolor nos dice que nos importa. De hecho, las relaciones pueden fortalecerse a partir de períodos de decepción.
Una amistad o una relación romántica puede superar muchos altibajos. A veces, durante nuestro dolor, puede parecer que nuestro afecto se ha desvanecido. A menudo, sin embargo, podemos volver a la cercanía porque nuestro dolor nos dice que nos importa. De hecho, las relaciones pueden fortalecerse a partir de períodos de decepción.
 ">
">


 ">
">

 ">
">

 ">
">

 ">
">

 ">
">


 ">
">

 ">
">


 ">
">


 ">
">
 ">
">
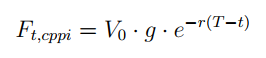
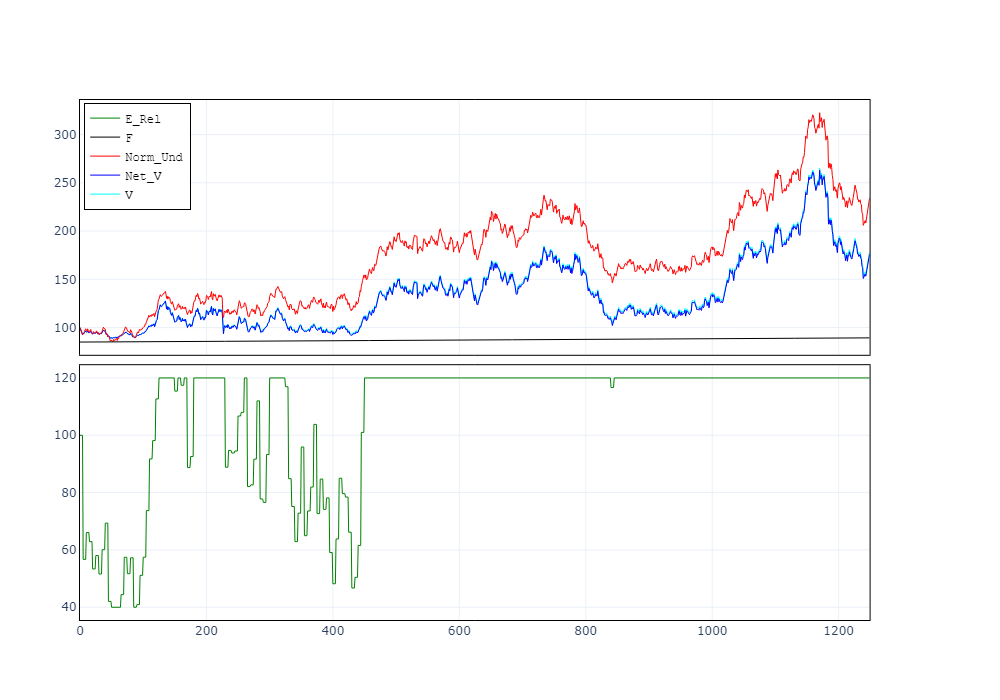
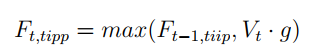
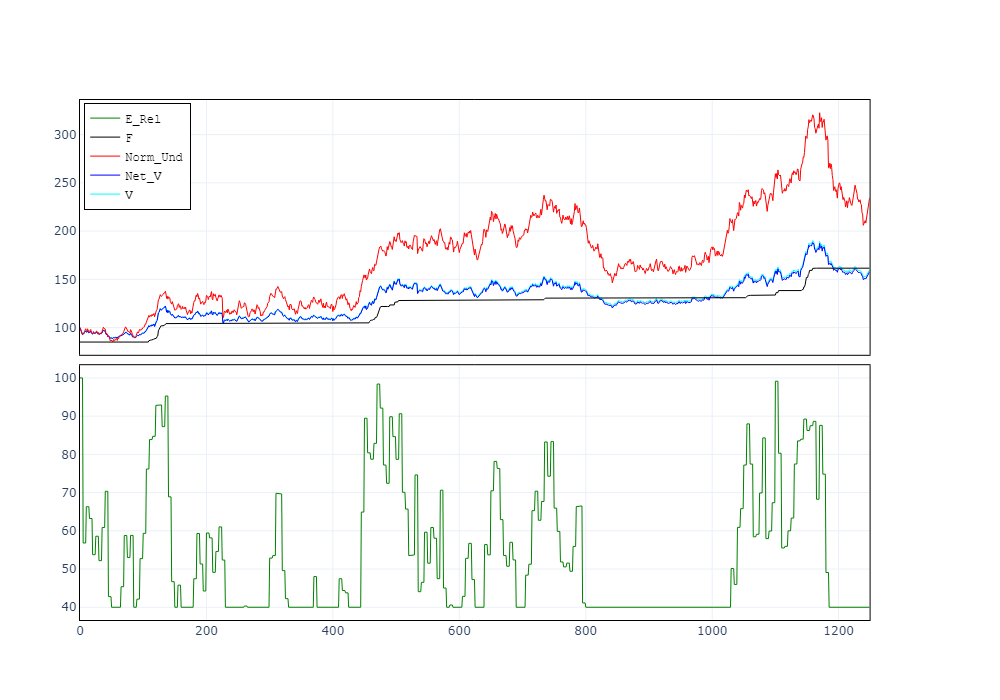

 ">
">