El valor de los factores sistemáticamente perdedores por Ignacio Villalonga

Ingeniero Aeronáutico por la Universidad Politécnica de Madrid, compagina su trabajo como analista de mercados en una importante empresa aeronáutica con los mercados financieros. Desarrollador de modelos de inversión cuantitativos de largo plazo, basados en factores. Autor del blog y del podcast Zona Quant. Profesor del Instituto Financiero Esfera Capital.
Ignacio Villalonga
/ Zona Quant
“I think being successful is just about not making mistakes. It’s not about having correct judgment. It’s about avoiding incorrect judgments”. The Almanack of Naval Ravikant
La mayoría de los inversores se pasa la vida pensando en el mejor sistema, la mejor cartera, la siguiente acción que va a ser un 100x bagger, la composición perfecta y otra serie de decisiones basadas en qué comprar, en tomar la decisión de mayor rentabilidad. Sin embargo, evitar aquellas inversiones que pueden ser las mayores perdedoras puede resultar mucho más beneficioso. Mi propuesta es filtrar primero acciones que sistemáticamente son perdedoras, para luego poder buscar las reglas ganadoras con mayor facilidad.
La vía negativa
En otras disciplinas, la implementación de la vía negativa como pilar primordial está muy extendido. En el mundo del fitness es mucho más frecuente escuchar sobre la importancia de eliminar hábitos negativos. En el venture capital o Private Equity, los inversores repiten una y otra vez que lo importante es decir que no a muchas empresas, porque su selección tiene que ser muy concreta. Gran parte de su éxito se basa en invertir en las empresas que “no” van a quebrar. La tasa es muy alta, y ahí es donde tienen la ventaja.
A la hora de diseñar carteras con acciones por factores, una herramienta muy potente es ser capaz de eliminar de tu universo elegible aquellas acciones que son sistemáticamente perdedoras. Esas acciones se camuflan en el universo de acciones porque no llaman tanto la atención. Suben cuando el mercado sube, bajan cuando el mercado baja, y se pierden entre la inmensidad del universo de acciones. Sin embargo, al fijarse bien, estas son perdedoras sistemáticamente respecto al resto de acciones.
Identificar factores sistemáticamente perdedores es tan importante como puede generar como identificar factores ganadores, siendo una herramienta muy potente para el inversor retail.
A lo largo de este artículo, me gustaría compartir con vosotros la importancia de filtrar bien en qué no querríamos invertir, para poder elegir bien luego lo que sí.
Voy a enfocarlo hacia una cartera de acciones, pero esto es aplicable a cualquier tipología de inversión.
Primero, lo básico
“Over the years, a number of very smart people have learned the hard way that a long string of impressive numbers multiplied by a single zero always equals zero.” Warren Buffett, carta a los accionistas de Berkshire Hathaway de 2005
Además de los factores sistemáticamente perdedores, en el mundo de la inversión, estos “ceros” también son costes altos, problemas de operabilidad, impuestos, apalancamiento excesivo, etc.
Por tanto, lo primero que debería filtrarse antes de empezar a realizar ninguna otra operación, son estos factores que hacen que simplemente operar la acción no merezca la pena. Si solo trabajáis con empresas de alta capitalización, no tendréis problema con esto. Pero para los que nos gusta buscar empresas desconocidas (donde hay más ventajas) es importante descartar aquellas que no son operables.
Estos filtros se aplican para asegurar que la acción tiene un volumen que la haga operable y que su precio tenga sentido sin deslizamientos inasumibles, que tenga información suficiente para estudiarla, etc. Todo esto estará muy ligado al tamaño de la cartera, de la posición y de las reglas de selección que vayas a escoger. Las empresas pequeñas tienen mas ineficiencias al estar menos estudiadas y presentan mayores potenciales. Sin embargo, también son de las que se dispone muchas veces menos información, y además, su volumen es más bajo, por lo que posiciones grandes pueden mover el precio y generando un sobrecoste que degrade los resultados del modelo.
Aunque parece básico, mucha gente hace estudios o backtests sin estos filtros primero, y obtiene resultados absolutamente idealizados. Y eso es una de las cosas que NO queremos.
Por supuesto estos filtros tienen además que ayudar a descartar cosas que pueden hacerte sentir incómodo. Por ejemplo, empresas que están en procesos de M&A, que tienen una OPA, que están tardando demasiado en reportar, o que van a reportar información dentro de muy poco tiempo y eso puede hacer que cambie tu análisis cambie antes de lo que te gustaría. Utiliza los filtros para descartar sorpresas con las que no quieres encontrarte.
Dando la vuelta al problema
“Subtractive knowledge: You know what is wrong with more certainty than you know anything else.” Nassim Taleb
Encontrar cual es el factor que hace que una empresa vaya a crecer más que las demás es muy complejo. Es difícil entender cuáles serán las tendencias del futuro, si la gente seguirá queriendo esa marca, si el management no tomará decisiones erróneas, o hasta cuándo podrás seguir creciendo, puesto que el límite de crecimiento es potencialmente “infinito”.
Sin embargo, encontrar factores que hacen que una empresa este sufriendo más que los demás es más sencillo, porque eventualmente las empresas tienen un límite de errores y, y al final que valgan cero y quiebren es algo más fácilmente identificable.

Factor sistemáticamente Perdedor
Un factor ganador sería aquel que al rankear las empresas, cuanto más arriba, es estadísticamente más probable que obtenga un rendimiento superior a la media. Puede ocurrir que muchas veces, a partir de cierto nivel, ya de igual. Es decir, el factor es capaz de separar a las ganadoras pero no igual de bien a las perdedoras, y debajo de determinado nivel los rendimientos son similares en cada decil.
Teniendo esto en la cabeza, un factor sistemáticamente perdedor sería aquel que identifica muy bien aquellas empresas que son sistemáticamente perdedoras, pero que por encima de determinado nivel las ganadoras no es capaz de identificarlas.
El factor ideal es aquel que es capaz de separar de tanto las ganadoras como las perdedoras
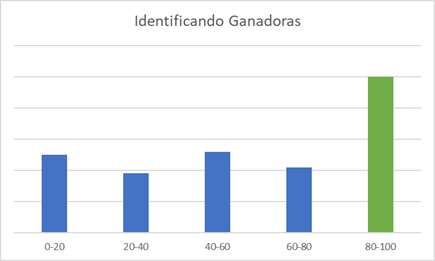
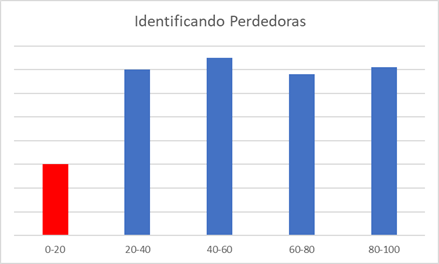
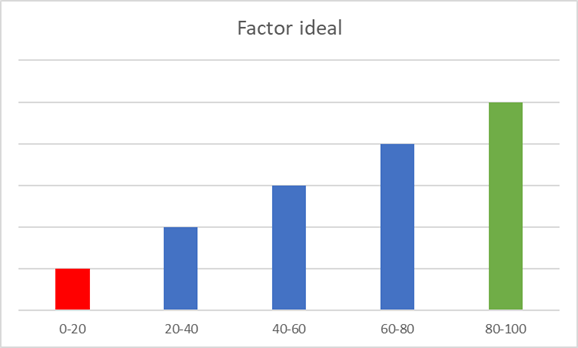
Esquema de resultados de factores en función de qué tipo de acciones es capaz de identificar: ganadoras, perdedoras o ambas.
Nota: un gráfico de cestas como el que mostramos se genera ordenando las acciones en función de un determinado factor y mirando su rendimiento en cada periodo de rebalanceo, donde vuelves a ordenar y a generar las cestas.
Ventajas en la amplitud del universo
Partir de universos de acciones que ya están filtrados con las acciones que no queremos que aparezcan tiene dos grandes ventajas:
- La primera es que, a la hora de seleccionar las acciones dentro de ese universo, vamos a partir de un sitio más seguro, y eso lleva a minimizar riesgos, mejorando el rendimiento. La parte negativa dentro de este punto es que encontrar un sistema de selección que genere alfa añadido será una tarea más compleja.
- El segundo punto y probablemente el más importante, es que a la hora de realizar los backtests, al haber aplicado los filtros de operabilidad, van a ser mucho más fiables, y tendrás más garantías de que los resultados se adecuaran más a la realidad. A parte, es probable que hayas eliminado outliers que distorsionaban los resultados.
Nota: hablamos de reducir la posibilidad, no de eliminar el riesgo por completo.
Ejemplo: Return on Equity
Todo esto tiene como objetivo mejorar la selección de cartera. Vamos a ver un ejemplo. Nosotros sabemos que el Return on Equity (RoE) es un factor de calidad. Y que las empresas con mejor RoE performan mejor. Pero, si vemos el gráfico de cestas aplicado al SP1500, vemos que la mayor diferencia no se da entre el Top 20% y el resto de cestas. La mayor diferencia se da entre el Peor 20% y el resto.
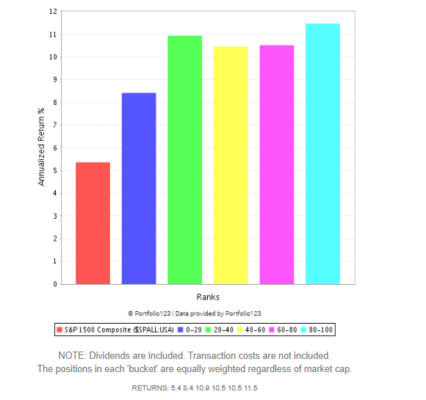
La imagen (5) anterior, son resultados realizados con una herramienta de Backtesting rebalanceando las cestas cada 4 semanas.
Para ver esto de forma un poco más intuitiva, podemos ver cómo se comportarían las carteras a lo largo del tiempo.
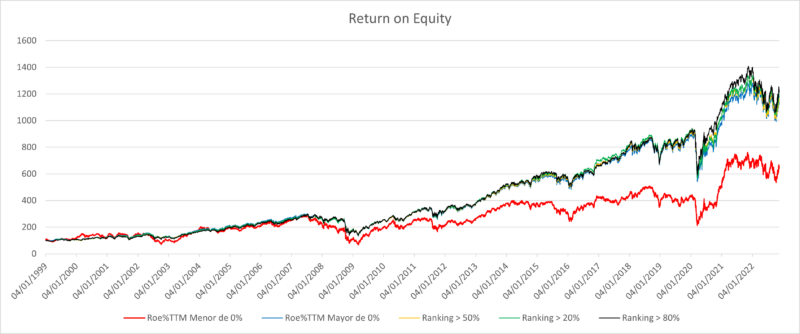
Podemos ver cómo lo que realmente aporta el factor es: Si la cartera está formada con las acciones cuyo RoE a doce meses (TTM) es mayor que cero, o si la cartera elimina el peor 20% de las acciones con peor RoE, los resultados son prácticamente idénticos. Incluso no se aprecia diferencia eliminar el 20% peor o el 50% peor. De hecho, el resultado apenas varía si se tomamos solamente el 20% de acciones con mayor RoE.
Básicamente, el valor está en descartar las que tienen un RoE negativo o muy bajo.
Ahora tienes un 80% de acciones de tu universo restante para poder elegir que comprar, sabiendo que entre ellas no estarán aquellas que son potencialmente sistemáticamente perdedoras.
En este caso, si solo te quedases con el top 20%, habrías eliminado muchas acciones sin obtener ningún tipo de ventaja ni beneficio.
De hecho, eliminar acciones de más es contraproducente cara al estudio y la relevancia estadística posterior.
Ejemplo Completo
Para generar un ejemplo concreto, vamos a tomar el universo Russell 3k y vamos a partir de una composición de cartera rebalanceada Equal Weight cada 4 semanas, con deslizamiento, comisiones y dividendos incluidos. Por supuesto, vemos que el no hacer nada y beneficiarse de una cartera Equal Weight con acciones operables ya aporta más de un 2,5% más de alfa. A partir de aquí, vamos a ir quitando grupos de acciones con la intención de ir mejorando el resultado final.
Terminamos eliminando aproximadamente dos tercios (2/3) del universo para pasar de un CAGR de 9,6% a 12,8%, que es más de un 33% más al año, que en el largo plazo marca una diferencia muy elevada.
Filtrar al principio es más sencillo, pero a medida que vas quitando acciones, es más difícil que el siguiente factor sea capaz de sacar mucha más ventaja, y elimine “nuevas” perdedoras. De hecho, en este caso se ve claramente que del filtrado Sentiment al siguiente, Growth 2, la diferencia es muy pequeña, y la media de acciones que elimina son 250 más, que es un 25%. Sin embargo, individualmente ambos producen mejoras similares.
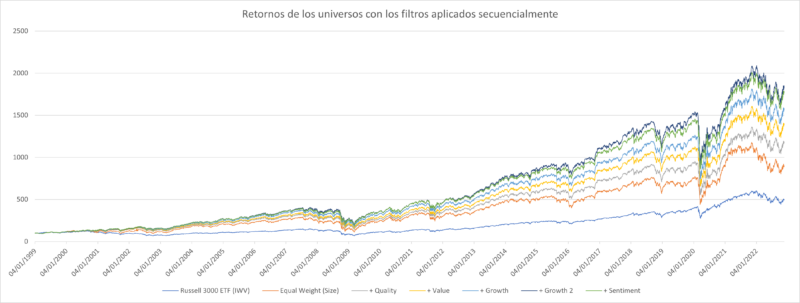

Los filtros utilizados han sido parámetros simples sobre los principales factores: Size, Value, Quality, Growth, y Sentimiento. Dentro de esto hemos generado una cartera rebalanceada Equal Weight, y le hemos metido filtros con RoE, Free Cash Flow, Operative Incomes, Yield y presión bajista sobre la empresa (Short Interest)
Conclusiones
Partiendo del universo final filtrado, podríamos empezar a buscar la forma de seleccionar una cartera de acciones para extraer más rentabilidad, partiendo de un punto donde estadísticamente, batir al benchmark va a ser mucho más sencillo porque hemos eliminado parte de las acciones que peor se comportan.
Esto genera una mecánica mucho más eficiente para diseñar carteras, donde la posibilidad de encontrar patrones ganadores es más alta.
En el ejemplo puesto, con filtros muy básicos, mejoramos el retorno sobre una cartera Equal Weight de todas las acciones en más de un 33% al año desde 1999. Dejamos además un tercio de todo el universo disponible para (+1000 acciones) para poder a pasar a la siguiente fase de selección de una cartera.
En este caso hemos utilizado factores que encuentran conjuntos de acciones sistemáticamente negativas. No obstante, también podrían usarse filtros binarios como el del ejemplo del RoE%TTM > 0. Estos filtros no eliminan un porcentaje de acciones peores o mejores según un factor, si no en función de si cumplen o no una caracteríssitica binaria.
El problema es que sabrás con menor exactitud (o menor aproximación) qué porcentaje de empresas eliminan en determinados momentos, siendo mucho más variable que la eliminación en función de un ranking. (Por ejemplo: en periodos bajistas poner filtros como “Beneficios crecientes” hace que el porcentaje de empresas que no pasen el filtro sea tan alto que no tenga relevancia estadística estudiar el universo que queda, por escasez de acciones a seleccionar). Como ventaja, es una regla mucho más precisa y conoces exactamente con qué nivel del factor estás descartando o no a las acciones.
Aunque todo esto lo he realizado con datos fundamentales, datos derivados del precio (Factor Momentum) y volatilidad pueden ser utilizados de forma eficiente también, siendo mucho más accesibles para cualquier inversor.
Por otra parte, al igual que al trabajar con factores sistemáticamente ganadores, es importante ver que son ganadores a lo largo del tiempo y en diferentes periodos. No analizar bien el factor y entender porque es sistemáticamente perdedor puede llevarnos a generar reglas en base a razones equivocadas. Y eso sí que es un gran error que hay que evitar.
 ">
">



 ">
">


 ">
">


 ">
">

 ">
">

 ">
">









 ">
">



 ">
">


 ">
">

 Para empezar este artículo comeremos «visualizando»
Para empezar este artículo comeremos «visualizando» 
 ">
">

 ">
">

 ">
">


 ">
">


 ">
">












 ">
">